Cho pt x2-2mx-m2-m+2=0
A/ tìm m để pt có nghiệm
B/tính x1+x2và x1×x2 theo m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 3 2022
a,để pt có nghiệm kép
\(\Delta=m^2-\left(m^2-m+1\right)=m-1=0\Leftrightarrow m=1\)
\(x_1=x_2=\dfrac{2m}{2}=m=1\)
b, để pt có nghiệm \(m\ge1\)
c, Ta có \(\left(x_1+x_2\right)^2-4x_1x_2=6\)
Thay vào ta đc \(4m^2-4\left(m^2-m+1\right)=6\)
\(\Leftrightarrow4m=10\Leftrightarrow m=\dfrac{5}{2}\left(tm\right)\)
7 tháng 8 2021
a) Thay m=-2 vào phương trình, ta được:
\(x^2+4x+3=0\)
a=1; b=4; c=3
Vì a-b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=-1;x_2=\dfrac{-c}{a}=-3\)
26 tháng 5 2022
a: \(\text{Δ}=\left(-6\right)^2-4\left(m+1\right)=-4m-4+36=-4m+32\)
Để phương trình có nghiệm thì -4m+32>=0
=>-4m>=-32
hay m<=8
b: Theo Vi-et,ta được:
\(\left\{{}\begin{matrix}x_1+x_2=6\\x_1x_2=m+1\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\)
\(\Leftrightarrow36-2\left(m+1\right)=20\)
=>2(m+1)=16
=>m+1=8
hay m=7(nhận)
2
26 tháng 5 2022
`a)` Ptr có nghiệm`<=>\Delta' >= 0`
`<=>(-3)^2-(m+1) >= 0`
`<=>9-m-1 >= 0<=>m <= 8`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`b)`Với `m <= 8`, áp dụng Viét có:`{(x_1+x_2=[-b]/a=6),(x_1.x_2=c/a=m+1):}`
Ta có:`x_1 ^2+x_2 ^2=20`
`<=>(x_1+x_2)^2-2x_1.x_2=20`
`<=>6^2-2(m+1)=20`
`<=>36-2m-2=20`
`<=>2m=14<=>m=7` (t/m)
2 tháng 4 2021
a) Thay m=1 vào phương trình, ta được:
\(x^2-2x+1+1^2-1=0\)
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)
hay x=1
Vậy: Khi m=1 thì tập nghiệm của phương trình là S={1}
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 12 2021
\(\Delta'=\left(m+1\right)^2-\left(m^2+3m-2\right)=-m+3\)
a. Phương trình có nghiệm khi:
\(\Delta'\ge0\Rightarrow m\le3\)
b. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+3m-2\end{matrix}\right.\)
c.
\(x_1^2+x_2^2-x_1x_2=22\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=22\)
\(\Leftrightarrow4\left(m+1\right)^2-3\left(m^2+3m-2\right)=22\)
\(\Leftrightarrow m^2-m-12=0\Rightarrow\left[{}\begin{matrix}m=4\left(loại\right)\\m=-3\end{matrix}\right.\)
CM
26 tháng 9 2017
Chọn C
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
pt (1) có 2 nghiệm thỏa mãn x1< 1< x2 khi và chỉ khi pt (2) có 2 nghiệm: t1< 0 < t2 suy ra P < 0
Hay m2- 3m+ 2 < 0
Do đó: 1 < m < 2
Kết luận: với 1< m< 2 thì pt (1) có hai nghiệm x1< 1< x2
CM
4 tháng 12 2019
Chọn D
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
pt (1) có 2 nghiệm thỏa x1< x2< 1 khi và chỉ khi pt (2) có 2 nghiệm:
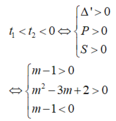
(vô nghiệm)
Kết luận: không tồn tại m thỏa mãn bài toán.
28 tháng 1
a: \(\text{Δ}=\left[-2\left(m+1\right)\right]^2-4\cdot1\cdot\left(m^2-4m+5\right)\)
\(=4\left(m+1\right)^2-4\left(m^2-4m+5\right)\)
\(=4m^2+8m+4-4m^2+16m-20\)
=24m-16
Để phương trình có hai nghiệm thì Δ>=0
=>24m-16>=0
=>24m>=16
=>\(m>=\dfrac{2}{3}\)
b: Bạn xem lại đề nha bạn
a,phương trình có nghiệm
`<=>\Delta>=0`
`<=>4m^2-4(m^2-m+2)>=0`
`<=>4m^2-4m^2+4m-8>=0`
`<=>4m>=8`
`<=>m>=2`
b,Áp dụng định lý vi-ét ta có:
`x_1+x_2=-b/a=2m`
`x_1.x_2=c/a=-m^2-m+2`