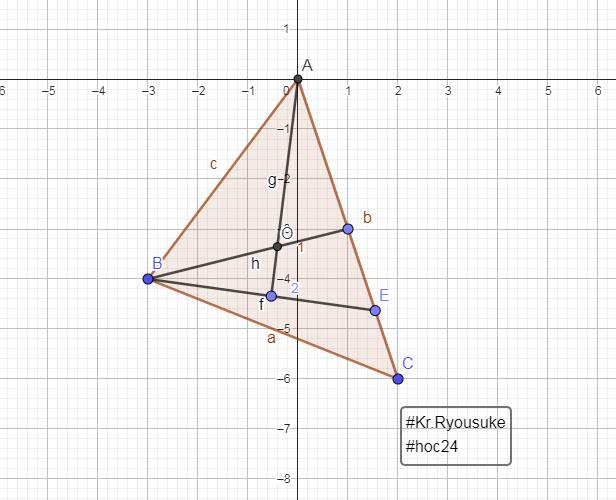
Trong ABC có AC> AB . Trên cạnh CA lấy điểm E sao cho CE = AB . Gọi O là
giao điểm của 2 đường trung trực của BE và AC. Chứng minh:
a.
b.
AO là tia phân giác của góc A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tg AOB và tg COE
AB = ce
oa = oc ( thuộc đường trung trực AC )
ob = oe ( .................................... Be )
suy ra = nhau
b, vì hai tg trên =
-> góc oab = góc oce 1
tg aoc cân tại o -> góc oac = góc oce 2
từ 1 , 2 suy ra góc oab = góc oac
suy ra đpcm

a; Ta có: O nằm trên đường trung trực của BE
nên OB=OE

Vì các đường trung trực của `\Delta ABC` cắt nhau tại điểm O
`->` `\text {AO}` là đường trung trực thứ `3` của `\Delta`
Xét các đáp án trên `-> D.`