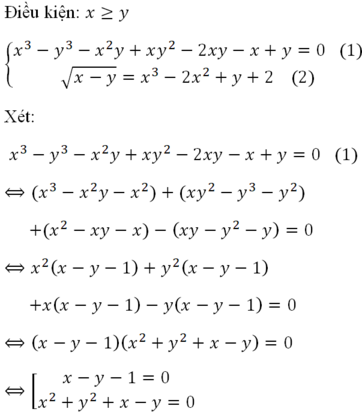Tìm nghiệm nguyên của phương trình sau
x3+x2y+2xy3=x2y2+y4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BN
0
Những câu hỏi liên quan
NS
0
PT
1
AH
Akai Haruma
Giáo viên
18 tháng 3 2021
Lời giải:
PT $\Leftrightarrow x^3+3x-5=x^2y+2y=y(x^2+2)$
$\Rightarrow y=\frac{x^3+3x-5}{x^2+2}$
Để $y$ nguyên thì $x^3+3x-5\vdots x^2+2$
$\Leftrightarrow x(x^2+2)+x-5\vdots x^2+2$
$\Leftrightarrow x-5\vdots x^2+2(1)$
$\Rightarrow x^2-5x\vdots x^2+2$
$\Leftrightarrow x^2+2-(5x+2)\vdots x^2+2$
$\Leftrightarrow 5x+2\vdots x^2+2(2)$
Từ $(1);(2)\Rightarrow 5(x-5)-(5x+2)\vdots x^2+2$
$\Leftrightarrow 27\vdots x^2+2$. Do $x^2+2\geq 2$ nên:
$\Rightarrow x^2+2\in\left\{3;9;27\right\}$
$\Rightarrow x^2\in\left\{1;7;25\right\}$
Do $x$ nguyên nên $x\in\left\{\pm 1; \pm 5\right\}$
Thay vào $y$ ta tìm được:
$x=-1\Rightarrow y=-3$
$x=5\Rightarrow y=5$
CM
10 tháng 6 2017
Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12
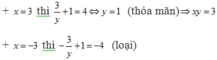
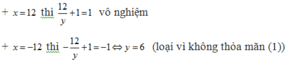
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
PT
1
CM
1 tháng 4 2019
Ta có: P = x2y + xy2 – 5x2y2 + x3 và Q = 3xy2 – x2y + x2y2
⇒ P + Q = (x2y + xy2 – 5x2y2 + x3) + (3xy2 – x2y + x2y2)
= x2y + xy2 – 5x2y2 + x3 + 3xy2 – x2y + x2y2
= x3 +(– 5x2y2 + x2y2)+ (x2y – x2y) + (xy2+ 3xy2)
= x3 – 4x2y2 + 0 + 4xy2
= x3 – 4x2y2 + 4xy2
18 tháng 7 2021
`(2x-y)(16x^4+8x^3y+4x^2y^2+2xy^3+y^4)`
`=(2x-y)[(2x)^4+(2x)^3y+(2x)^2y^2+2xy^3+y^4)`
`=(2x)^5-y^5`
`=32x^5-y^5`
CM
24 tháng 6 2017
Ta có P + Q=x2 y + xy2 - 5x2 y2 + x3 + 3xy2 - x2 y + x2 y2
= -4x2 y2 + x3 + 4xy2
Chọn B
NT
2
HP
20 tháng 2 2021
\(\left\{{}\begin{matrix}2x^3+x^2y=3\left(1\right)\\2y^3+xy^2=3\end{matrix}\right.\)
Trừ vế theo vế hai phương trình ta được:
\(2\left(x^3-y^3\right)+\left(x^2y-xy^2\right)=0\)
\(\Leftrightarrow2\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(2x^2+3xy+2y^2\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left[2\left(x+\dfrac{9}{16}y\right)^2+\dfrac{7}{8}y^2\right]=0\left(2\right)\)
Do \(2\left(x+\dfrac{9}{16}y\right)^2+\dfrac{7}{8}y^2\ge0\), đẳng thức xảy ra khi \(x=y=0\)
Thay vào phương trình ta thấy \(x=y=0\) không phải là nghiệm
\(\Rightarrow2\left(x+\dfrac{9}{16}y\right)^2+\dfrac{7}{8}y^2>0\)
Khi đó \(\left(2\right)\Leftrightarrow x=y\)
\(\left(1\right)\Leftrightarrow2x^3+x^3=3\Leftrightarrow x=y=1\)
\(\Rightarrow x_0^3+y_0^3=2\)