Cho hình bình hành ABCD và đường thẳng d không cắt các cạnh của hình bình hành. Gọi A',B',C',D' lần lượt là hình chiếu của A,B,C,D lên d. Chứng minh AA' + CC' = BB' + DD'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 10 2016
Gọi O là giao điểm của hai đường chéo AC và BD. Từ O kẻ OM song song với CI , suy ra OM cũng song song với KD và BH
Ta có \(\hept{\begin{cases}OA=OC\\OM\text{//}CI\end{cases}\Rightarrow}\)OM là đường trung bình tam giác ACI => \(CI=2OM\left(1\right)\)
Lại có \(\hept{\begin{cases}DK\text{//}OM\text{//}BH\\OD=OB\end{cases}\Rightarrow}\)OM là đường trung bình của hình thang BHKD
\(\Rightarrow KD+BH=2OM\left(2\right)\)
Từ (1) và (2) suy ra \(BH+CI+DK=4OM\le4OA\left(\text{hằng số}\right)\)
Vậy \(BH+CI+KD\) đạt giá trị lớn nhất bằng 4OA khi \(\hept{\begin{cases}OM=OA\\OM\perp d\end{cases}}\Rightarrow\)đường thẳng d vuông góc với CA tại A
CM
27 tháng 5 2019
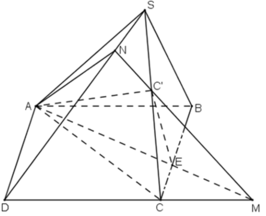
a) Giao điểm M của CD và mp(C’AE).
Trong mp(ABCD), d cắt CD tại M, ta có:
+ M ∈ CD
+ M ∈ d ⊂ (C’AE) ⇒ M ∈ (C’AE)
Vậy M là giao điểm của CD và mp(C’AE).
b) + Trong mặt phẳng (SCD), gọi giao điểm của MC’ và SD là N.
N ∈ MC’ ⊂ (C’AE) ⇒ N ∈ (C’AE).
N ∈ SD ⊂ (SCD) ⇒ N ∈ (SCD)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
+ (C’AE) ∩ (SCB) = C’E.
+ (C’AE) ∩ (SAD) = AN.
+ (C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE
17 tháng 11 2016
Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành. Từ O hạ đường cao OO' vuông góc với d tại O'.
Ta có \(\hept{\begin{cases}OA=OC\\OO'\text{//}AH\end{cases}\Rightarrow}\) OO' là đường trung bình của tam giác AHC => AH = 2OO' (1)
Xét tứ giác BDKI có : \(\hept{\begin{cases}DK\text{//}OO'\text{//}BI\\OB=OD\end{cases}\Rightarrow}\) OO' là đường trung bình của hình thang BDKI
=> DK + BI = 2OO' (2)
Từ (1) và (2) suy ra AH = BI + DK.
Bạn sửa lại đề bài cho đúng nhé!
17 tháng 11 2016
Gọi F là giao điểm của AH và BC. Kẽ DF vuông góc với AH
Ta có \(\widehat{AEH}=\widehat{AHC}=\widehat{DKC}=90\)
\(\Rightarrow DEHK\)là hình chữ nhật
\(\Rightarrow HE=DK\left(1\right)\)
Ta có \(\widehat{DAF}=\widehat{AFB\:}\)(AD // BC)
\(\widehat{IBF}=\widehat{AFB\:}\)(BI // AH)
\(\Rightarrow\widehat{DAF}=\widehat{IBF}\)
\(\widehat{AFD}=\widehat{BIC}=90\)
AD = BC
\(\Rightarrow\Delta BIC=\Delta AED\)
\(\Rightarrow BI=AE\left(2\right)\)
Từ (1) và (2) => AE + HE = AH = BI + DK
PS: Phải là chứng minh AH = BI + DK mới đúng nha
Q
31 tháng 3 2017
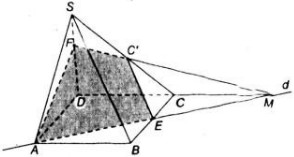
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE).
b)
Do M = DC ∩ (C'AE) nên M ∈ (SDC),.
Trong (SDC) : MC' ∩ SD = F.
Ta có:
\(\left(C'AE\right)\cap\left(SDC\right)=FC'\)
\(\left(C'AE\right)\cap\left(SAD\right)=AF\)
\(\left(C'AE\right)\cap\left(ABCD\right)=AE\)
\(\left(C'AE\right)\cap\left(SBC\right)=C'E\)
Vậy thiết diện là AEC'F.
tham khảo
18 tháng 12 2022
a Xét tứ giác DEBF có
BE//DF
BE=FD
Do đó; DEBF là hình bình hành
=>DB cắt EF tại trung điểm của mỗi đường(1)
b: Vì ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mõi đường(2)
Từ (1), (2) suy ra AC,BD,EF đồng quy
=>E,O,F thẳng hàng
ai giúp mình với