Cho Tam giác ABC. trên cạnh AB,AC lấy các điểm B' ,C' sao cho AB'/AB=AC'/AC
a, so sánh AC và A'C'
b, chứng minh B'C'//BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 2 2020
Lời giải :
Ta có : \(\frac{AB'}{AB}=\frac{AC'}{AC}\)( GT ) ( 1 )
+) Đường thẳng a đi qua B' song song với BC ( GT )
\(B'C''//BC\)( vì đường thẳng a cắt AC tại C'' )
\(\Rightarrow\frac{AB'}{AB}=\frac{AC''}{AC}\)( Định lí Ta lét ) ( 2 )
Từ ( 1 ) và ( 2 )
\(\Rightarrow AC'=AC''\)
CM
10 tháng 12 2017
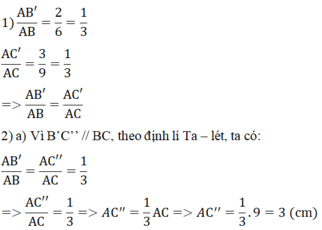
b) Trên đoạn thẳng AC ta có: AC’= AC’’= 3 cm nên
Khi đó, hai đường thẳng BC và B’C’ song song với nhau.
F
15 tháng 9 2019
Bài giải
a, Ta có : AB' là tia đối của AB ; AB = AB'
AC' là tia đối của AC ; AC = AC'
\(\Rightarrow\text{ Hai góc }ABC\text{ và }AB'C'\text{ là hai góc đối đỉnh}\)
\(\Rightarrow\text{ }\widehat{ABC}=\widehat{AB'C'}\)
\(\Rightarrow\text{ }BC=B'C'\)
b, Chịu
Anh https://olm.vn/thanhvien/dang91920071q làm giùm nha !
30 tháng 9 2019
a. Xét \(\Delta\)AB'C' và \(\Delta\)ABC có:
AB = AB' ;
^B'AC' = ^BAC;
AC = AC' ;
=> \(\Delta\)AB'C' = \(\Delta\)ABC ( c-g-c)
=> BC = B'C' (1)
b) Xét \(\Delta\)ABM và \(\Delta\)AB'M' có:
^ABM = ^AB'M' ( \(\Delta\)AB'C' = \(\Delta\)ABC )
AB' = AB (gt)
^BAM = ^B'AM ( đối đỉnh)
=> \(\Delta\)ABM và \(\Delta\)AB'M'
=> BM = B'M' (2)
Từ (1); (2) => BC - BM = B'C' - B'M'
=> CM = C'M' (3)
mà M là trung điểm BC => MB = MC (4)
(2); (3); (4) => B'M' = M'C'
=> M' là trung điểm B'C'
24 tháng 2 2021
a) Ta có: \(\dfrac{AN}{AB}=\dfrac{3}{6}=\dfrac{1}{2}\)
\(\dfrac{AM}{AC}=\dfrac{4.5}{9}=\dfrac{1}{2}\)
Do đó: \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)\(\left(=\dfrac{1}{2}\right)\)
Xét ΔANM và ΔABC có
\(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔANM\(\sim\)ΔABC(c-g-c)
