Cả câu này nữa ạ mk cảm ơn nhiều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)

Nếu các bạn đưa câu hỏi trắc nghiệm có đầy đủ hướng dẫn, câu hỏi của bạn sẽ được chọn để đưa vào phần câu hỏi trắc nghiệm của HOC24. Khi đó điểm GP của bạn sẽ được tăng thêm 3 đ.

a) \(x^2+xy+x\)
\(=x\left(x+y+1\right)\)
Thay x=77, y=22
\(=77\left(77+22+1\right)\)
\(=77.100=7700\)
b) \(x\left(x-y\right)+y\left(y-x\right)\)
\(=\left(x-y\right)\left(x-y\right)\)
\(=\left(x-y\right)^2\)
Thay x=53, y=3
\(=\left(53-3\right)^2\)
\(=50^2=2500\)
c) \(x\left(x-1\right)-y\left(1-x\right)\)
\(=\left(x+y\right)\left(x-1\right)\)
Thay x=2021, y=2029
\(=\left(2021+2019\right)\left(2021-1\right)\)
\(=4040.2020\)
\(=8160800\)


1/
1. although
2. around
3. where
4. forward
5. and
6. will
2/ 1B 2F 3E 4A 5D 6C
3/
1. daily
2. wearing
3. would do
4. haven't eaten
5. is being carried
6. rises
7. inexperienced
8. equality
4/
1. which -> who
2. pollute -> polluting
5/
1. not to touch that
2. Tom has met is
3. weren't ill
4. may be built
6/
1. environmentalists
2. affect
3. media
4. responsible
7/
1. T
2. T
3. F
4. F



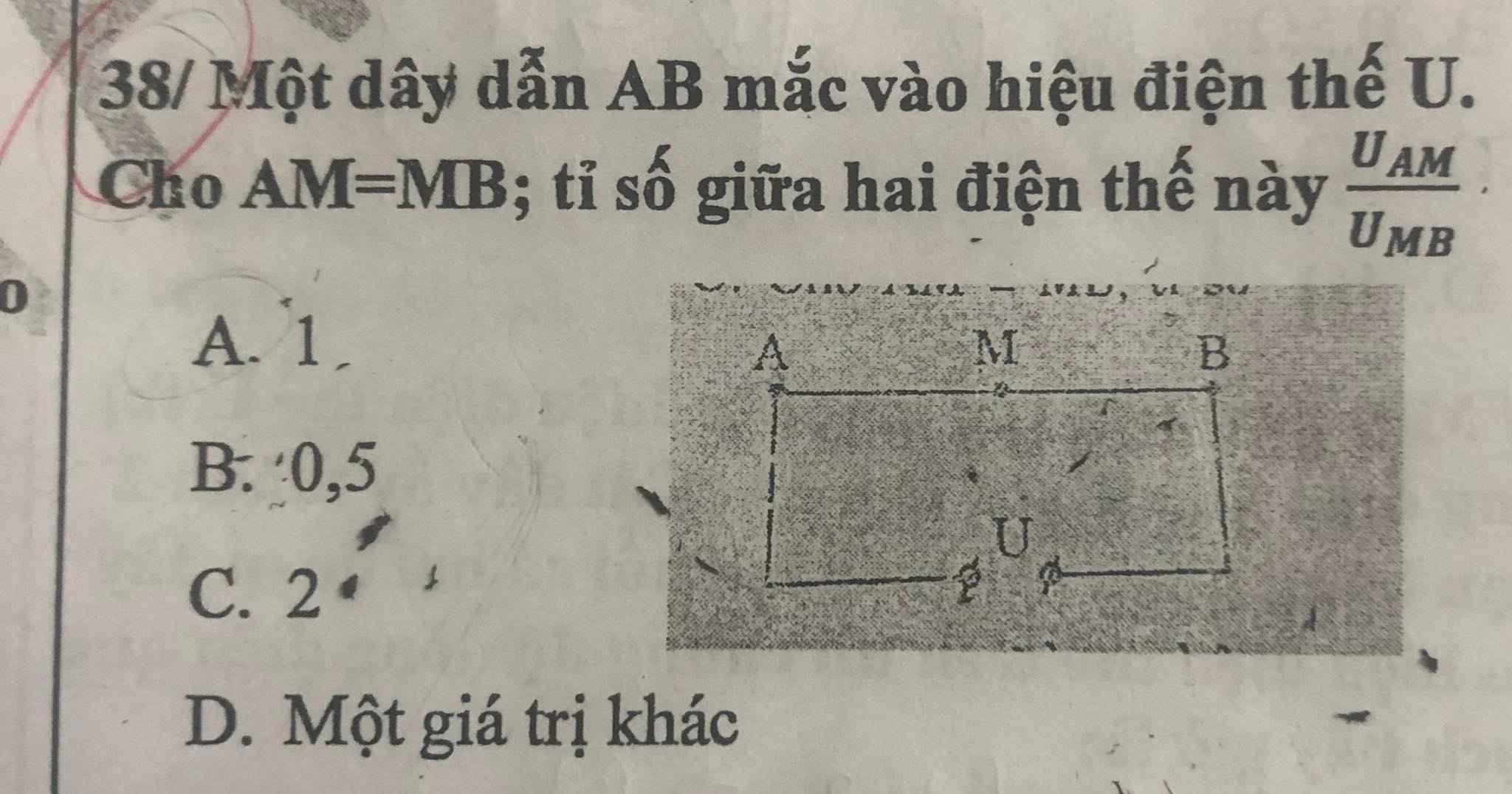
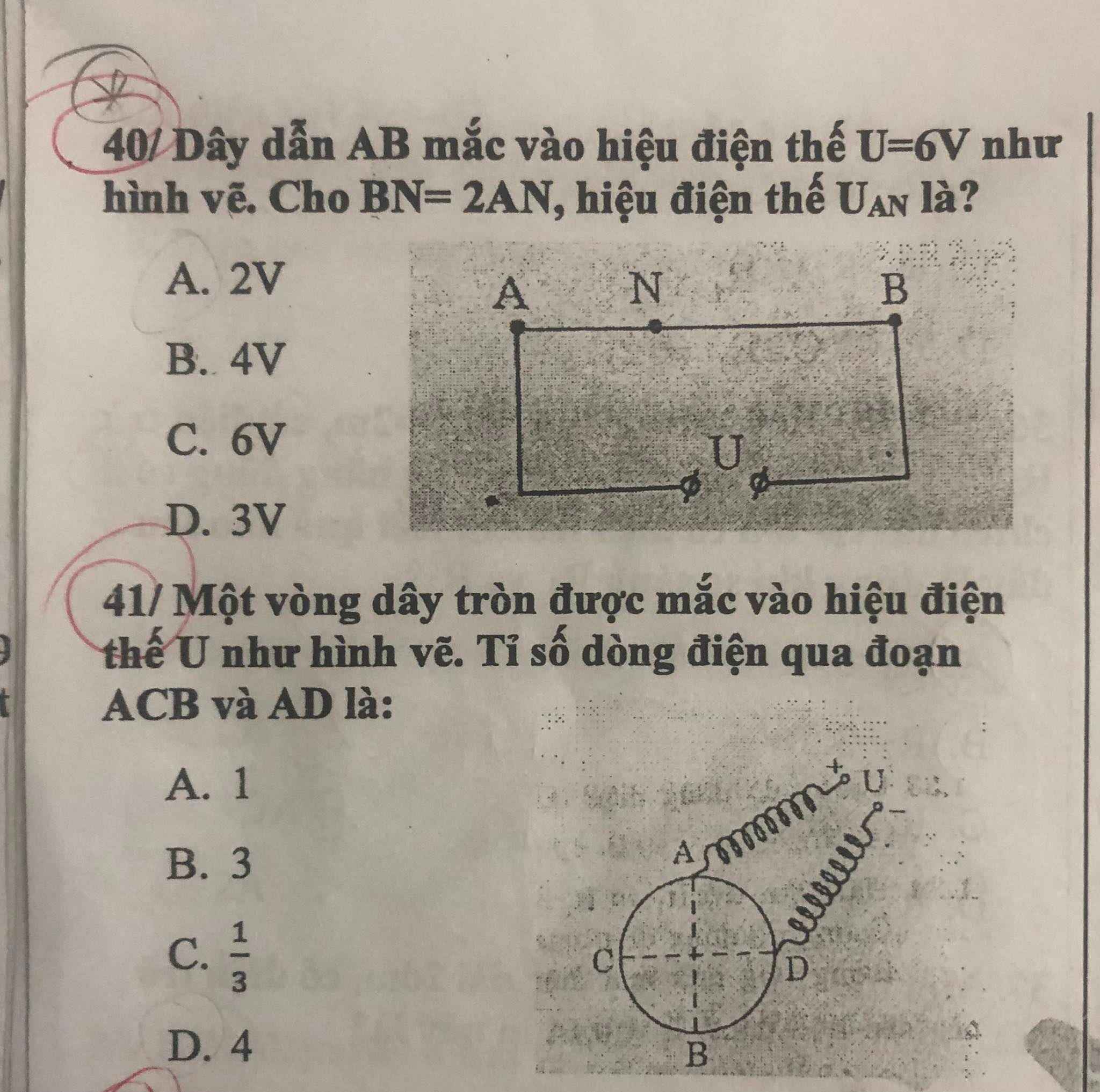

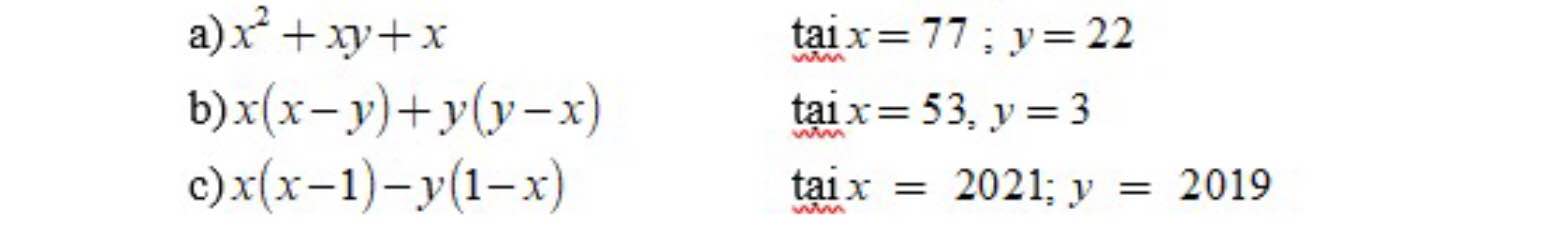 bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ
bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ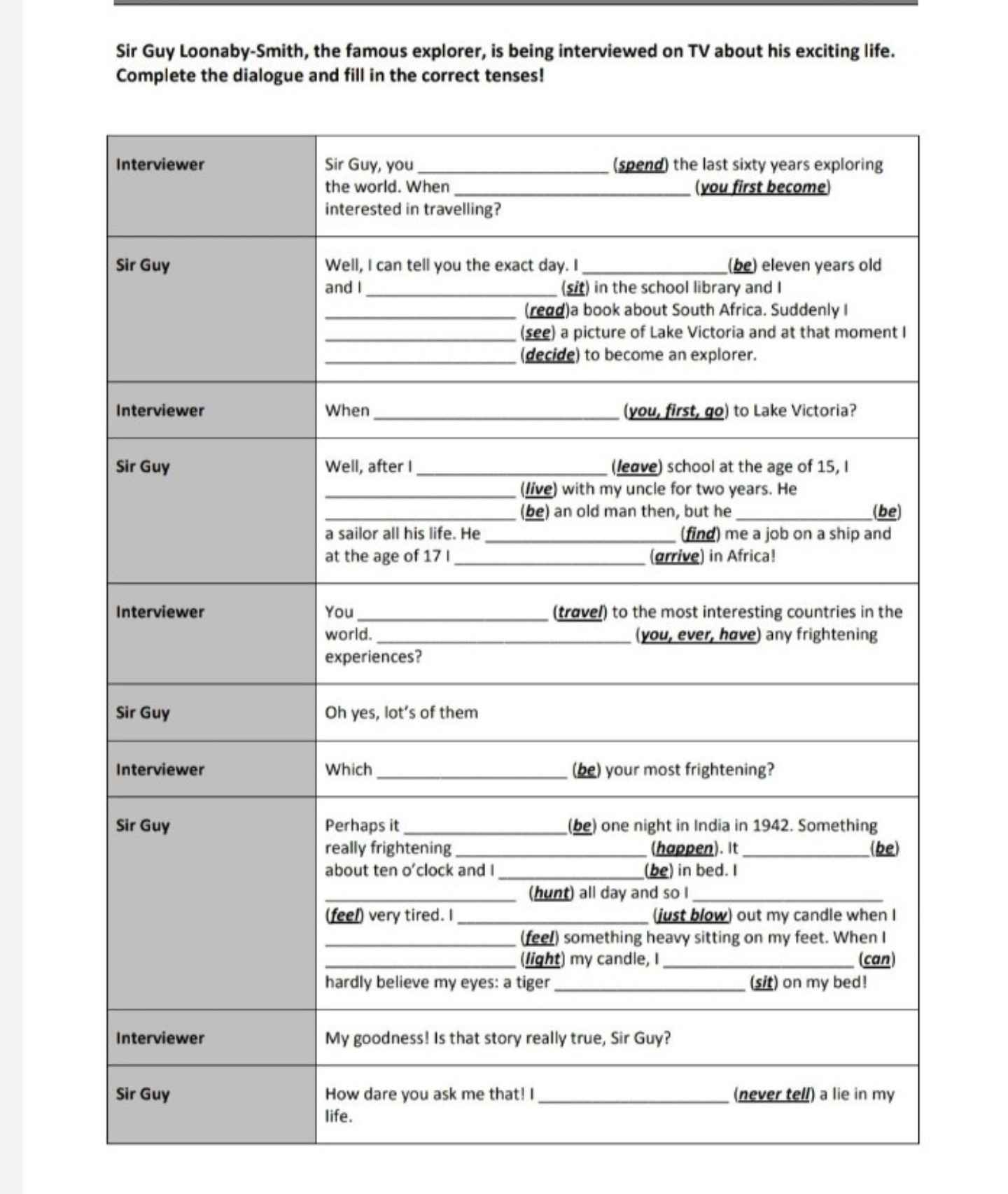

Ta thấy x=0 không là nghiệm của pt
Chia cả 2 vế cho \(x^2\ne0\) ta được:
\(x^4+\text{ax}^3+bx^2+cx+1=0\)
\(\Leftrightarrow x^2+\dfrac{1}{x^2}+\text{ax}+b+\dfrac{c}{x}=0\)
\(\Leftrightarrow x^2+\dfrac{1}{x^2}=-\text{ax}-b-\dfrac{c}{x}\)
\(\Rightarrow\left(x^2+\dfrac{1}{x^2}\right)^2=\left(\text{ax}+\dfrac{c}{x}+b\right)^2\le\left(a^2+b^2+c^2\right)\left(x^2+\dfrac{1}{x^2}+1\right)\)
( theo BĐT Bunhiacopxki)
\(\Rightarrow\left(a^2+b^2+c^2\right)\ge\dfrac{\left(x^2+\dfrac{1}{x^2}\right)^2}{x^2+\dfrac{1}{x^2}+1}\ge\dfrac{4}{3}\)( theo bánh Cosi)
Dấu '=' xảy ra khi \(x^2=\dfrac{1}{x^2}\Leftrightarrow x=\pm1\)
==> Chọn A