cho tam giác abc gốc a vuông gọi m là trung điểm của bc, N là trung điểm cạnh AC. Các đường thằng MN và AC cắt nhau tại G.
a) So sánh Sagn với Sbmg
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 2 2021
a) Ta có: \(AM=MB=\dfrac{AB}{2}\)(M là trung điểm của AB)
\(AN=NC=\dfrac{AC}{2}\)(N là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AM=MB=AN=NC
Xét ΔAMO vuông tại M và ΔANO vuông tại N có
AO chung
AM=AN(cmt)
Do đó: ΔAMO=ΔANO(cạnh huyền-cạnh góc vuông)
b) Ta có: ΔAMO=ΔANO(cmt)
nên \(\widehat{MAO}=\widehat{NAO}\)(hai góc tương ứng)
hay \(\widehat{BAH}=\widehat{CAH}\)
mà tia AH nằm giữa hai tia AB,AC
nên AH là tia phân giác của \(\widehat{BAC}\)
c) Xét ΔAHB và ΔAHC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}=\widehat{CAH}\)(cmt)
AH chung
Do đó: ΔAHB=ΔAHC(c-g-c)
Suy ra: HB=HC(hai cạnh tương ứng)
Ta có: ΔAHB=ΔAHC(cmt)
nên \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
hay \(AH\perp BC\)(đpcm)
22 tháng 2 2021
Hình vẽ : tự vẽ
a) Ta có : tan giác ABC cân tại A ( gt )
\(\Rightarrow\) \(\left\{{}\begin{matrix}AB=AC\\\widehat{B}=\widehat{C}\end{matrix}\right.\)( t/c \(\Delta\) cân )
Ta có : AB = AC ( cmt )
Mà : M là trung điểm của AB ( gt ), N là trung điểm của AC ( gt )
\(\Rightarrow\dfrac{1}{2}AB=\dfrac{1}{2}AC\)
\(\Rightarrow AM=AN\)
Xét : \(\Delta\)AMO và \(\Delta\)ANO có
Cạnh AO chung
AM =AN (cmt )
\(\widehat{AMO}=\widehat{ANO}=90^0\left(CM\perp AB,BN\perp AC\right)\)
\(\Rightarrow\Delta AMO=\Delta ANO\left(ch-cgv\right)\)
b) Có \(\Delta AMO=\Delta ANO\left(cmt\right)\)
\(\Rightarrow\widehat{MAO}=\widehat{NAO}\) ( 2 cạnh tương ứng )
Ta có :
\(\widehat{MAO}=\widehat{NAO}\left(cmt\right)\)
Mà : Tia AH nằm giữa tia AB và tia AC
\(\Rightarrow\) AH là tia phân giác của \(\widehat{A}\) ( đpcm )
c) Ta có :
\(\Delta ABC\) cân tại A ( gt ), AH là tia phân giác của \(\widehat{A}\) ( cmt )
\(\Rightarrow\) AH cùng là đường cao và trung truyến
\(\Rightarrow\left\{{}\begin{matrix}AH\perp BC\\HB=HC\end{matrix}\right.\)( tính chất đường cao và trung tuyến )
d) Ta có :
\(AH\perp BC\left(cmt\right)\)
\(\Rightarrow\widehat{OHC}=90^0\)
\(\Rightarrow\)OC lớn hơn HC
Mà HC = HB ( cmt )
\(\Rightarrow\) OC lớn hơn HB ( đpcm )
-Hết-
15 tháng 5 2023
`@` `\text {dnv4510}`
`a,`
Xét `\Delta ABC:`
`\text {BC > AC > AB (5 cm > 4 cm > 3 cm)}`
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`=>` $\widehat {A} > \widehat {B} > \widehat {C}$.
`b,`
Ta có: A là trung điểm của BD
`-> \text {AC là đường trung tuyến}` `(1)`
K là trung điểm của BC
`-> \text {DK là đường trung tuyến}` `(2)`
Mà \(\text{AC }\cap\text{ DK = M}\) `(3)`
Từ `(1), (2)` và `(3)`
`-> \text {M là trọng tâm của} \Delta ABC`
`@` Theo tính chất của trọng tâm trong `\Delta`
\(\text{MC = }\dfrac{2}{3}\text{AC}\)
Mà \(\text{AC = 4 cm}\)
`->`\(\text{MC = }\dfrac{2}{3}\cdot4=\dfrac{8}{3}\left(\text{cm}\right)\)
Vậy, độ dài của MC là `8/3 cm`
`b,`
Ta có: \(\left\{{}\begin{matrix}\text{A là trung điểm của BC}\\\text{AC }\bot\text{ BD}\end{matrix}\right.\)
`->`\(\text{CA là đường trung trực}\)
Ta có: \(\left\{{}\begin{matrix}\text{AC là đường trung trực (hạ từ đỉnh A)}\\\text{AC là đường trung tuyến (hạ từ đỉnh A) }\end{matrix}\right.\)
`@` Theo tính chất của các đường trong `\Delta` với `\Delta` cân
`->` \(\Delta\text{ BDC cân tại C (đpcm).}\)
15 tháng 5 2023
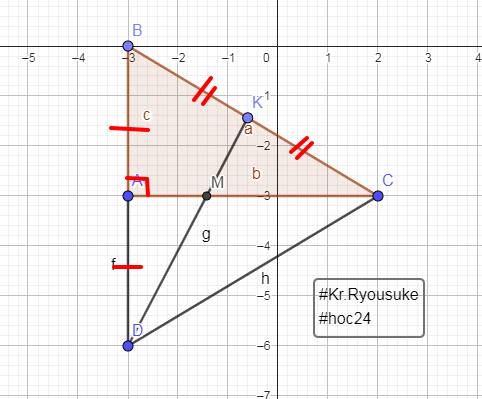
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCBD có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=8/3cm
c: Xét ΔCBD co
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
11 tháng 8 2023
a: Xét ΔABC có AB<AC<BC
nên góc C<góc B<góc A
b: Xét ΔCDB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=16/3(cm)
c: Gọi giao của d với AC là N
d là trung trực của AC
=>d vuông góc AC tại N và N là trung điểm của AC
=>QN//AD
Xét ΔCAD có
N là trung điểm của AC
NQ//AD
=>Q là trung điểm của CD
Xét ΔCDB có
BQ là trung tuyến
M là trọng tâm
=>B,M,Q thẳng hàng
11 tháng 8 2023
a, Ta có: AB < AC < BC
=> C < B< A
b, Xét tam giác BCD có CA và DK là đường trung tuyến
CA cắt DK tại M
=> M là trọng tâm tam giác BCD
=> MC= 2/3 AC= 2/3.8= 16/3 cm
c, Xét tam giác ABC và tam giác ADC có:
AB = AD
BAC= DAC= 90°AC chung
=> tam giác ABC = tam giác ADC (c.g.c)
=> ACB= ACD (2 góc tương ứng) và BC = DC ( 2 cạnh tương ứng) (1)
KQ là đường trung trực của AC
=> KQ vuông góc với AC tại E
Xét tam giác KCE và tam giác QCE có:
KCE= QCE
EC chung
KEC= QEC=90°
=> tam giác KCE = tam giác QCE (gcg)
=> KC = QC (2 cạnh tương ứng) (2)
Mà K là trung điểm BC (3)
Từ (1), (2) và (3) suy ra Q là trung điểm của DC
Xét tam giác BCD có M là trong tâm
=> M thuộc đường trung tuyến BQ
=> B, M, Q thẳng hàng
17 tháng 4 2023
a: AB<AC<BC
=>góc C<góc B<góc A
b: XétΔCDB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3*8=16/3cm
27 tháng 4 2023
a: Xét ΔBAE và ΔBME có
BA=BM
AE=ME
BE chung
=>ΔBAE=ΔBME
b: Xet ΔBAK và ΔBMK có
BA=BM
góc ABK=góc MBK
BK chung
=>ΔBAK=ΔBMK
=>góc BMK=90 độ
=>MK vuông góc AC
c: Xét tứ giác KFMQ có
MF//KQ
MF=KQ
=>KFMQ là hình bình hành
=>MQ//FK
=>góc CMQ=góc CBK=góc ABK