Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Áp dụng định lí Pytago vào tam giác ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100 nên BC =10 cm
Ta có: AB < AC < BC ( 6 cm < 8 cm < 10 cm )
Do đó, dây BC gần tâm nhất, dây AB xa tâm nhất

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó:ΔACB vuông tại C
=>\(\widehat{ACB}=90^0\)
Ta có: ΔOAC cân tại O(OA=OC)
mà OH là đường trung tuyến
nên OH\(\perp\)AC và OH là tia phân giác của góc AOC
Ta có: OH\(\perp\)AC(cmt)
AC\(\perp\)CB tại C(Do ΔACB vuông tại C)
Do đó: OH//BC
b:
OH là phân giác của góc AOC
=>\(\widehat{AOH}=\widehat{COH}\)
mà M\(\in\)OH
nên \(\widehat{AOM}=\widehat{COM}\)
Xét ΔOCM và ΔOAM có
OC=OA
\(\widehat{COM}=\widehat{AOM}\)
OM chung
Do đó: ΔOCM=ΔOAM
=>\(\widehat{OCM}=\widehat{OAM}\)
mà \(\widehat{OCM}=90^0\)
nên \(\widehat{OAM}=90^0\)
=>OA\(\perp\)MA tại A
=>MA là tiếp tuyến tại A của (O)

Đáp án C
Tam giác ABC có góc A là góc tù nên 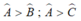
Mà cạnh đối diện với góc A là cạnh BC .
Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:
BC > AC và BC > AB
Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.
Chưa thể kết luận dây nào xa tâm nhất.
Vì \(\Delta ABC\)vuông tại A nội tiếp đường tròn (O;R) nên O là trung điểm của BC.
\(\Rightarrow BC=2OB=2R=2.3=6\left(cm\right)\)
\(\Delta ABC\)vuông tại A \(\Rightarrow AC=BC.\sin B\)\(=6.\frac{2}{3}=4\left(cm\right)\)
\(\Delta ABC\)vuông tại A \(\Rightarrow BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=6^2-4^2=36-16=20\)
\(\Rightarrow AB=\sqrt{20}\left(cm\right)\)(1)
Ta có \(AC=4cm=\sqrt{16}cm\)(2)
Từ (1) và (2) \(\Rightarrow AB>AC\)
Xét đường tròn (O) có 2 dây AB, AC và \(AB>AC\left(cmt\right)\Rightarrow\)Dây AB gần tâm hơn dây AC (liên hệ giữa dây và khoảng cách từ tâm đến dây)
b) Dễ thấy O là trung điểm BC và OI//AC\(\left(\perp AB\right)\)\(\Rightarrow\)I là trung điểm AB\(\Rightarrow\)OI là đường trung bình của \(\Delta ABC\)
\(\Rightarrow OI=\frac{AC}{2}=\frac{4}{2}=2\left(cm\right)\)
Mặt khác I là trung điểm AB \(\Rightarrow IB=\frac{AB}{2}=\frac{\sqrt{20}}{2}=\sqrt{5}\left(cm\right)\)
Xét đường tròn (O)
sinB = \(\frac{AC}{BC}=\frac{2}{3}\)(*)
mà BC là đường kình, O là trung điểm => OC = 3 cm => BC = 2OC = 6 cm
Thay vào (*) ta được : \(\frac{AC}{6}=\frac{2}{3}\Rightarrow AC=4\)cm
Theo định lí Pytago tam giác ABC vuông tại A
\(AB=\sqrt{BC^2-AC^2}=\sqrt{36-16}=2\sqrt{5}\)cm
Gọi d(O;AB) = OH ; d(O;AC) = OK
Ta có AC > AB ( 4 > \(2\sqrt{5}\)) => OK < OH
b, đề có sai ko bạn
Nếu ABC vuông tại A => AC vuông AB
OH vuông AB => OH // AC mà qua O kẻ đường thẳng song song AC cắt AB tại I ???