Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, A D B ^ là góc nội tiếp trên đường kính AB => A D ⊥ B D
b, Do
A
D
C
^
=
90
0
nên DÎ đường tròn (k;
A
C
2
)
c, ∆IBD cân tại I có B ^ = 60 0 => ∆IBD đều => B I D ^ = 60 0
=> l B D ⏜ = π . 5 2 . 60 180 = 5 6 π cm

a: Xét (O) có
ΔAHB nội tiếp
AB là đường kính
=>ΔAHB vuông tại H
=>AH vuông góc BC
b: ΔHAC vuông tại H nên ΔAHC nội tiếp đường tròn đường kính AC
=>KA=KH=KC
Xét ΔKAO và ΔKHO có
KA=KH
AO=HO
KO chung
=>ΔKAO=ΔKHO
=>góc KHO=góc KAO=90 độ

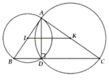
\(1,\)Gọi I là tâm đường tròn đường kính BC thì I là trung điểm BC và \(MI=IN=BI=CI=\dfrac{1}{2}BC\) (bán kính cùng đường tròn)
\(\Rightarrow\Delta BNC\) vuông tại N và \(\Delta CMB\) vuông tại N
Vậy \(\widehat{BMC}=\widehat{BNC}=90\) độ
\(2,\)Ta có \(H=BM\cap CN\)
Mà BM, CN là đường cao tam giác ABC
Suy ra H là trực tâm
\(\Rightarrow AH\) là đường cao thứ 3
\(\Rightarrow AH\perp BC\)
\(3,\) Gọi giao điểm của tiếp tuyến tại N và AH là K, AH cắt BC tại E.
Ta có \(\widehat{KNH}+\widehat{INH}=90\)
Mà \(\widehat{INH}=\widehat{NCI}\left(NI=IC\right)\)
\(\Rightarrow\widehat{KNH}+\widehat{NCI}=90\)
Mà \(\widehat{NCI}+\widehat{CHE}=90\)
\(\Rightarrow\widehat{KNH}=\widehat{CHE}\)
Mà \(\widehat{CHE}=\widehat{NHK}\left(đđ\right)\)
\(\Rightarrow\widehat{KNH}=\widehat{NHK}\)
\(\Rightarrow\Delta NHK\) cân tại K\(\Rightarrow NK=KH\left(1\right)\)
Ta có \(\widehat{KNH}+\widehat{KNA}=90;\widehat{KHN}+\widehat{NAH}=90\)
\(\Rightarrow\widehat{ANK}=\widehat{NAK}\Rightarrow NK=AK\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow NK=KH=AK\)
\(\Rightarrow\)Đfcm
Tick plzzz, nghĩ nát óc đó
1: Xét (O) có
\(\widehat{BNC}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{BNC}=90^0\)
Xét (O) có
\(\widehat{BMC}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{BMC}=90^0\)
2: Xét ΔABC có
BM là đường cao ứng với cạnh AC
CN là đường cao ứng với cạnh AB
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
Suy ra: AH\(\perp\)BC
Gọi M, N, P lần lượt là trung điểm BC, CA, AB
Ta có: \(\left\{{}\begin{matrix}BM=\dfrac{1}{2}BC\\BP=\dfrac{1}{2}AB\\AB=BC\end{matrix}\right.\) \(\Rightarrow BM=BP\)
\(\Rightarrow\Delta BMP\) cân tại B
Mà \(\widehat{B}=60^0\) (do tam giác ABC đều) \(\Rightarrow\Delta BMP\) đều
\(\Rightarrow MB=MP\)
Hoàn toàn tương tự, ta có tam giác CMN đều \(\Rightarrow MC=MN\)
\(\Rightarrow MB=MC=MP=MN\)
\(\Rightarrow B;C;P;N\) cùng thuộc đường tròn tâm M hay đường tròn đường kính BC đi qua trung điểm AB, AC