Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
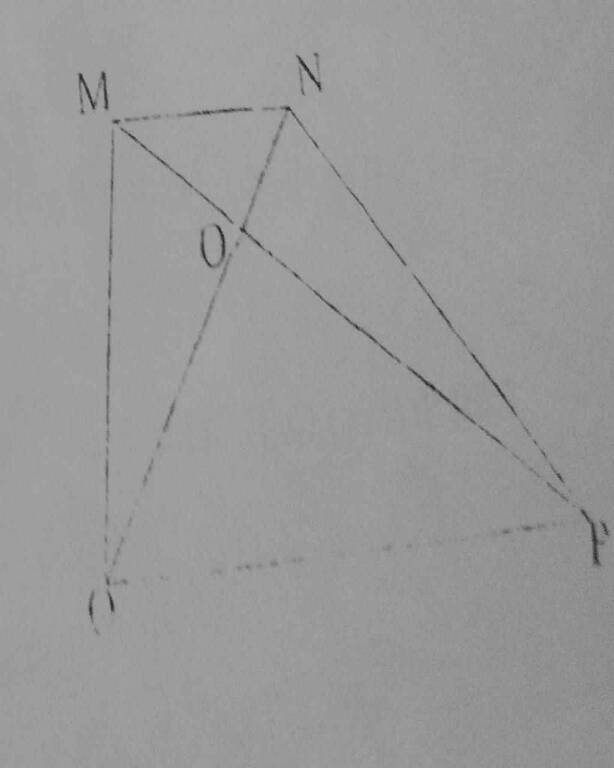
$S_{MNQ}=S_{MNP}$ (do chiều cao bằng nhau và chung đáy)
$\Rightarrow S_{MQK}=S_{NKP}=15$ (cm2)
Kẻ đường cao $NH$ xuống $MP$, đường cao $QT$ xuông $MH$
\(\frac{S_{MNP}}{S_{MQP}}=\frac{MN}{PQ}=\frac{3}{5}\)
\(\frac{S_{MNP}}{S_{MQP}}=\frac{NH}{QT}\)
\(1=\frac{S_{NPK}}{S_{MQK}}=\frac{NH\times PK}{QT\times MK}\Rightarrow \frac{NH}{QT}=\frac{MK}{PK}\)
Từ 3 điều trên suy ra $\frac{MK}{PK}=\frac{3}{5}$
$\frac{S_{MNK}}{S_{NPK}}=\frac{MK}{PK}=\frac{3}{5}$
$S_{MNK}=\frac{3}{5}\times S_{NPK}=\frac{3}{5}\times 15=9$ (cm2)
$\frac{S_{MQK}}{S_{PQK}}=\frac{MK}{PK}=\frac{3}{5}$
$\Rightarrow S_{PQK}=\frac{5}{3}\times S_{MQK}=\frac{5}{3}\times 15=25$ (cm2)
Diện tích hình thang:
$15+15+9+25=64$ (cm2)

a: Xét tứ giác MNKP có
MN//KP
MP//NK
=>MNKP là hình bình hành
=>MP=NK
mà MP=NQ
nên NK=NQ
=>ΔNKQ cân tại N
b: MNKP là hbh
=>góc K=góc NMP
=>góc K=góc MPQ
=>góc MPQ=góc NQP
Xét ΔMQP và ΔNPQ có
MP=NQ
góc MPQ=góc NQP
QP chung
=>ΔMQP=ΔNPQ
c: ΔMQP=ΔNPQ
=>góc MQP=góc NPQ
=>MNPQ là hình thang cân