Question

[An Sơ Hạ]

Biết ₁ʃ² lnx/x² dx = b/c + aln2 ( với a là số thực, b,c là số nguyên dương và b/c là phân số tối giản. Tính giá trị của 2a + 3b + c

Answer 1

[Hoàng Tử Hà]

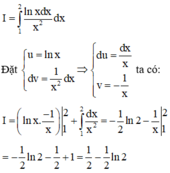
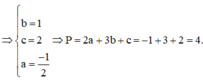
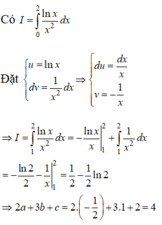
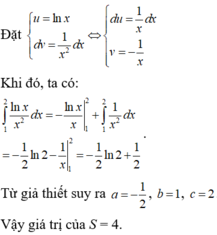
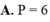
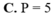
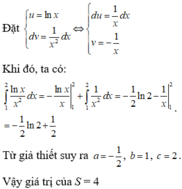
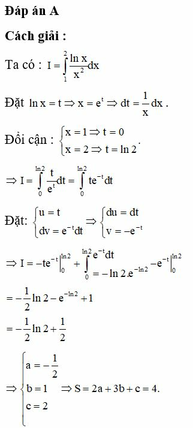
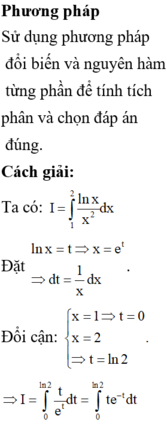
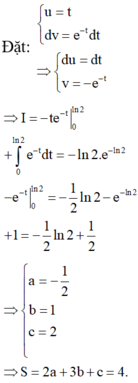
\(\int\limits^2_1\dfrac{lnx}{x^2}.dx\)

Dat \(\left\{{}\begin{matrix}u=lnx\\dv=\dfrac{dx}{x^2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=-\dfrac{1}{x}\end{matrix}\right.\)

\(\Rightarrow\int\limits^2_1\dfrac{lnx}{x^2}dx=lnx.\left(-\dfrac{1}{x}\right)|^2_1+\int\limits^2_1\dfrac{1}{x^2}.dx\)

\(=lnx.\left(-\dfrac{1}{x}\right)|^2_1+\left(-\dfrac{1}{x}\right)|^2_1=\left(-\dfrac{1}{2}\right).ln2+ln1-\dfrac{1}{2}+1\)

\(=\dfrac{1}{2}-\dfrac{1}{2}ln2\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=1\\c=2\end{matrix}\right.\Rightarrow P=2a+3b+c=-1+3+2=4\)