Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\int\limits^2_1\frac{8x+5}{6x^2+7x+2}dx=\int\limits^2_1\frac{8x+5}{6\left(x+\frac{1}{2}\right)\left(x+\frac{2}{3}\right)}dx=\frac{1}{6}\int\limits^2_1(\frac{2}{x+\frac{2}{3}}+\frac{6}{x+\frac{1}{2}})dx\:\)
\(=\frac{1}{6}\left(2ln\left|x+\frac{1}{2}\right|+6ln\left|x+\frac{2}{3}\right|\right)\)\(|^2_1\)
=\(\frac{1}{3}ln\left(\left|x+\frac{1}{2}\right|\right)+ln\left(\left|x+\frac{2}{3}\right|\right)\)\(|^2_1\)
= \(\frac{1}{3}ln\frac{5}{2}+ln\frac{8}{3}-\frac{1}{3}ln\frac{3}{2}-ln\frac{5}{3}=\frac{1}{3}ln5-\frac{1}{3}ln3+ln8-ln3=3ln2-\frac{4}{3}ln3+\frac{1}{3}ln5\)
\(\Rightarrow\)a=3,b=\(\frac{-4}{3}\),c=\(\frac{1}{3}\)
P=2

\(H=\int\limits^3_2\frac{1}{x^2\left(x+1\right)}dx\)
Sử dụng hệ số bất định để tách biểu thức tích phân:
\(\frac{1}{x^2\left(x+1\right)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}=\frac{Ax\left(x+1\right)+B\left(x+1\right)+Cx^2}{x^2\left(x+1\right)}=\frac{\left(A+C\right)x^2+\left(A+B\right)x+B}{x^2\left(x+1\right)}\)
Đồng nhất 2 vế ta được: \(\left\{{}\begin{matrix}A+C=0\\A+B=0\\B=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A=-1\\B=C=1\end{matrix}\right.\)
\(\Rightarrow H=\int\limits^3_2\left(-\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\right)dx=\left(-lnx-\frac{1}{x}+ln\left(x+1\right)\right)|^3_2=3ln2-2ln3+\frac{1}{6}\)
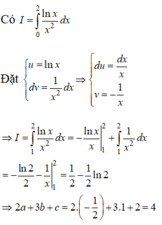
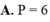

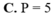

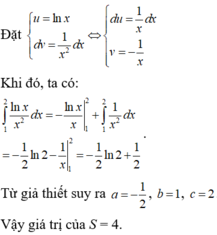
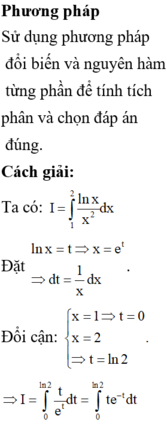
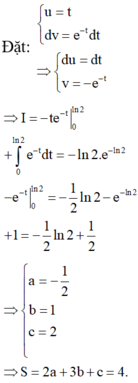
\(\int\limits^2_1\dfrac{lnx}{x^2}.dx\)
Dat \(\left\{{}\begin{matrix}u=lnx\\dv=\dfrac{dx}{x^2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=-\dfrac{1}{x}\end{matrix}\right.\)
\(\Rightarrow\int\limits^2_1\dfrac{lnx}{x^2}dx=lnx.\left(-\dfrac{1}{x}\right)|^2_1+\int\limits^2_1\dfrac{1}{x^2}.dx\)
\(=lnx.\left(-\dfrac{1}{x}\right)|^2_1+\left(-\dfrac{1}{x}\right)|^2_1=\left(-\dfrac{1}{2}\right).ln2+ln1-\dfrac{1}{2}+1\)
\(=\dfrac{1}{2}-\dfrac{1}{2}ln2\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=1\\c=2\end{matrix}\right.\Rightarrow P=2a+3b+c=-1+3+2=4\)