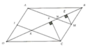
Cho hình chữ nhật ABCD có diện tích là S. Gọi M là trung điểm của BC, DM cắt AC tại N.
a)Tính diện tích ABMD theo S.
b)Tính diện tích ABMN theo S
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 3 2017
a) Kẻ BH vuông góc với AD.
SABCD=BH.AD=BH.2BM=S
=> BH.BM=\(\dfrac{S}{2}\)
Có AD song song với BM (ABCD là hbh)
SABMD=\(\dfrac{\left(AD+BM\right).BH}{2}=\dfrac{3BM.BH}{2}=\dfrac{3}{2}.\dfrac{S}{2}=\dfrac{3S}{4}\)
b) Nối A với M. T là trung điểm của AD. Nối B với T.
Ta có: TDMB là hbh (TD song song với BM; TD=BM=\(\dfrac{1}{2}BC\))
=> TF là đường TB của tam giác ADN => AF=FN (1)
MN là đường TB của tam giác BCF => FN=NC (2)
Từ (1)(2)=> AF=FN=NC
Ta có: SNMC=SFMN=SAFM
mà SABC =\(\dfrac{S}{2}\) và SABM=SACM => SAMC= \(\dfrac{S}{4}\)
=> SMNC = \(\dfrac{S}{4}:3=\dfrac{S}{12}\)
=> SABMN = SABC-SMNC = \(\dfrac{S}{2}-\dfrac{S}{12}=\dfrac{5S}{12}\)
CM
4 tháng 3 2019
Gọi I là trung điểm của AD, K là giao điểm của CI và BD. Kẻ ME ^ BD tại E, CF ^ BD tại F.
Có B N = 1 3 B D , E M = 1 2 C F S B M N = 1 2 E M . B N = 1 2 . 1 2 C F . 1 3 B D = 1 6 S B C D = 1 12 S ⇒ S M N D C = 1 2 S − 1 12 S = 5 12 S
A
21 tháng 2 2022
xét tam giác AMC và tam giác MBN có
góc AMC = góc NMB ( đối đỉnh )
AM = MB ( giả thiết )
góc A = góc B = 90 độ
nến tám giác AMC = tam giác MBN mà tam giác ta có
diện tích tam giác AMC= 168cm2 mà diện tích tám giác AMC = 1/4 diện tích HCN ABCD
nến ta có diện thích hình chữ nhật ABCD = 168*4 = 672cm2
kết luận : diện tích HCN ABCD =672cm2
CM
18 tháng 9 2019
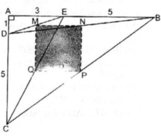
△ DMC có CM = 2/3BC
Hình bình hành ABCD và ΔDMC có chung đường cao kẻ từ đỉnh D đến BC.
Gọi độ dài đường cao là h, BC = a
Ta có diện tích hình bình hành ABCD là S = a h
S D M C = 1/2 h. 2/3 a = 1/3 ah = 1/3 S
S A B M D = S A B C D - S D M C = s - 1/3 S = 2/3 S
GV
Giáo viên Toán
Giáo viên
29 tháng 4 2017
a) dt(ABMD) = dt(ABCD) - dt(CMD)
Mà dt(CMD) = 1/2 MC.h = 1/2 . 2/3 . BC .h = 1/3 dt(ABCD) = 1/3.S
(với h là đường cao hạ từ A xuống BC của hình bình hành ABCD)
Suy ra dt(ABMD) = S - 1/3 S = 2/3. S
b) dt(ABNT) = BN.h = 2/3 BC . h = 2/3 . S
a) Kẻ BH vuông góc với AD.
SABCD=BH.AD=BH.2BM=S
=> BH.BM=S2S2
Có AD song song với BM (ABCD là hbh)
SABMD=(AD+BM).BH2=3BM.BH2=32.S2=3S4(AD+BM).BH2=3BM.BH2=32.S2=3S4
b) Nối A với M. T là trung điểm của AD. Nối B với T.
Ta có: TDMB là hbh (TD song song với BM; TD=BM=12BC12BC)
=> TF là đường TB của tam giác ADN => AF=FN (1)
MN là đường TB của tam giác BCF => FN=NC (2)
Từ (1)(2)=> AF=FN=NC
Ta có: SNMC=SFMN=SAFM
mà SABC =S2S2 và SABM=SACM => SAMC= S4S4
=> SMNC = S4:3=S12S4:3=S12
=> SABMN = SABC-SMNC = S2−S12=5S12