cho tam giác ABC vuông tại a có ah vuông góc với BC, trên cạnh AB, AC lấy 2 điểm E, D sao cho góc DHE=90 độ. Tìm vị trí của điểm D, E sao cho độ dài DE nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 4 2020
a,Xét tg ABC có: Góc A=90*,Góc M=90*,Góc N=90* <=>Tứ giác AMDN là hcn(vì có gócA=góc M=góc N=90*)
S
12 tháng 7 2018
a, Xét t/g AHC và t/g DHC có:
AH = DH (gt)
góc AHC = góc DHC = 90 độ
HC chung
=> t/g AHC = t/g DHC (c.g.c) (đpcm)
b, Áp dụng định lí pytago vào t/g ABC vuông tại A ta có:
AB2 + AC2 = BC2
=> AC2 = BC2 - AB2 = 102 - 62 = 64 = 82
=> AC = 8 (cm)
c, Xét t/g AHB và t/g DHE có:
AH = DH (gt)
góc AHB = góc DHE (đối đỉnh)
BH = EH (gt)
=> t/g AHB = t/g DHE (c.g.c) (đpcm)
=> góc HBA = góc DEH (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> AB // DE
Mà AB _|_ AC
=> DE _|_ AC (đpcm)
d, Vì t/g AHC = t/g DHC (câu a) => AC = CD (2 cạnh tương ứng) (1)
Xét t/g AHB và t/g AHE có:
BH = BE (gt)
góc AHB = góc AHE = 90 độ
AH chung
=> t/g AHB = t/g AHE (c.g.c)
=> AB = AE (2 cạnh tương ứng) (2)
Xét t/g ABC có: AB + AC > BC (BĐT tam giác) (3)
Từ (1),(2),(3) => AE + CD > BC (đpcm)
CM
5 tháng 2 2017
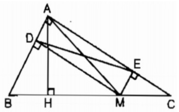
Ta có: AH ⊥ BC nên AM ≥ AH (quan hệ đường vuông góc và đường xiên)
Dấu “=” xảy ra khi M trùng với H
Mà DE = AM ( chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC
18 tháng 3 2021
a)áp dụng định lý Py-Ta-Go cho ΔABC vuông tại A
ta có:
BC2=AB2+AC2
BC2=62+82
BC2=36+64=100
⇒BC=\(\sqrt{100}\)=10
vậy BC=10
AB và AC không bằng nhau nên không chứng minh được bạn ơi
còn ED và AC cũng không vuông góc nên không chứng minh được luôn
Xin bạn đừng ném đá
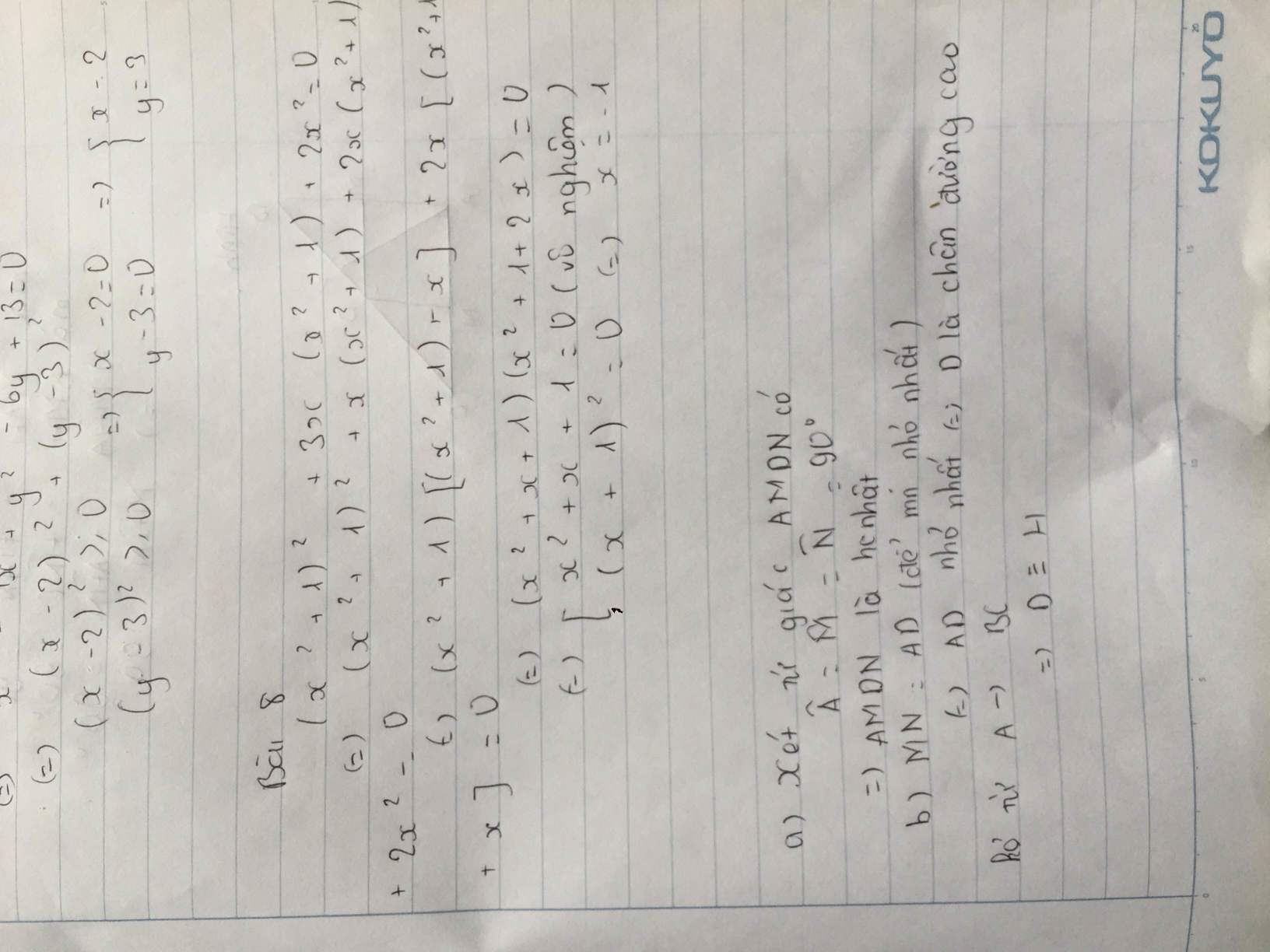
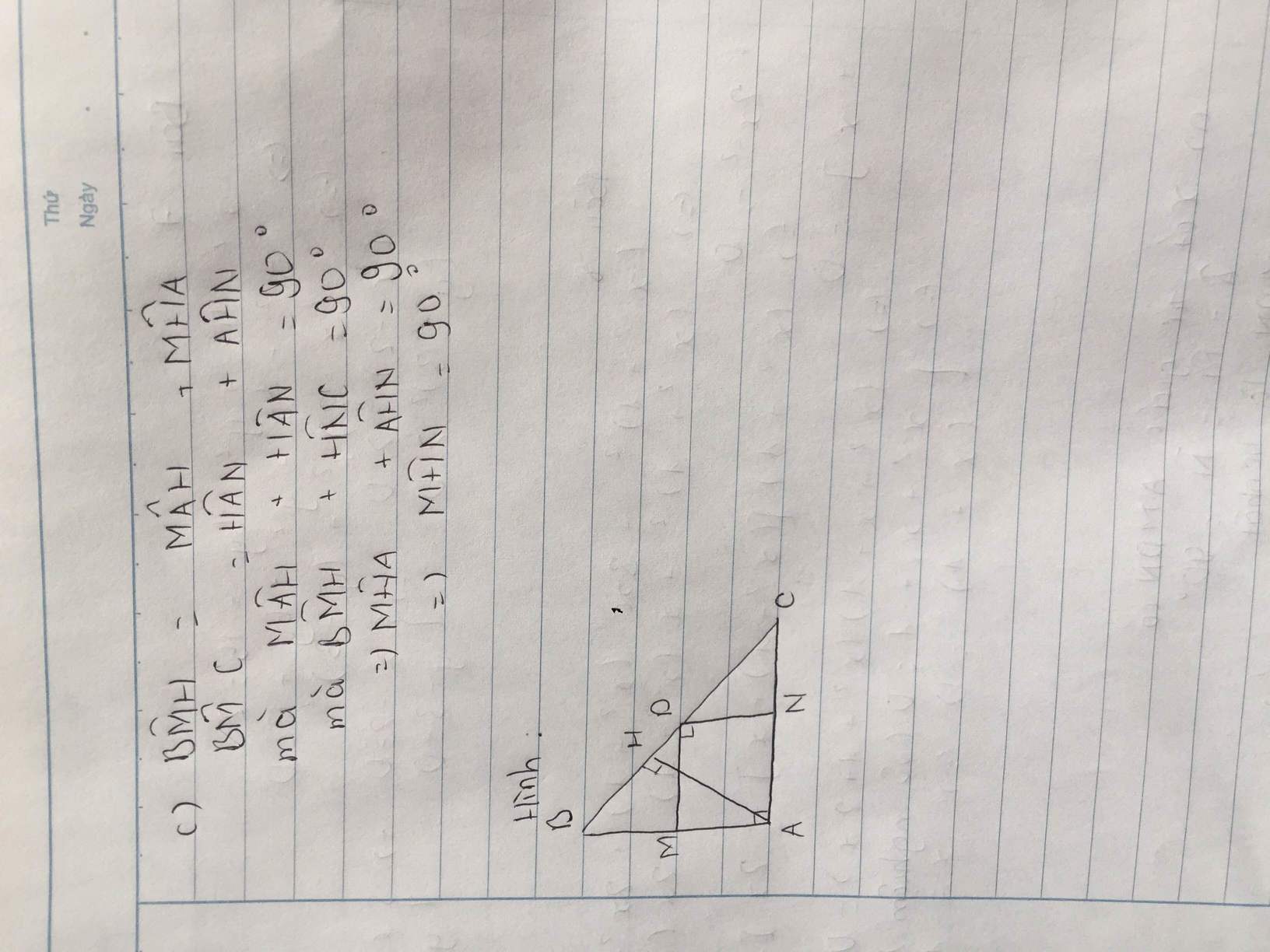
Nếu HE song song với AC thì tứ giác ADHE là hình chữ nhật, do đó DE = AH.
Nếu HE không song song với AC. Gọi M là giao điểm của HE với AC.
Ta có: \(\Delta MEA\sim\Delta MDH(g.g)\Rightarrow \frac{ME}{MA}=\frac{MD}{MH}\Rightarrow \Delta MAH\sim\Delta MED\Rightarrow \frac{DE}{AH}=\frac{ME}{MA}>1\Rightarrow DE>AH\).
So sánh hai trường hợp, ta có DEmin = AH khi HE song song với AC.