\(u_1=1\)
\(u_{n+1}=un+2n+1\)
dự đoán un và chứng minh quy nạp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Năm số hạng đầu của dãy số
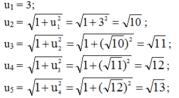
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
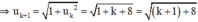
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.

Dễ dàng nhận ra dãy đã cho là dãy dương.
\(\Rightarrow u_1u_2...u_{n-1}>0\Rightarrow u_n>1\) ;\(\forall x>1\)
\(\Rightarrow u_1u_2...u_{n-1}>1\)
Ta có:
\(u_{n+1}-u_n=1+u_1u_2...u_n-u_n=1+u_n\left(u_1u_2...u_{n-1}\right)>0\)
\(\Rightarrow u_{n+1}>u_n\Rightarrow\) dãy tăng

Lời giải:
Ta có:
\((\sqrt{n+1}+\sqrt{n})U_n=\frac{2}{2n+1}\)
\(\Rightarrow U_n=\frac{2}{(2n+1)(\sqrt{n+1}+\sqrt{n})}=\frac{2(\sqrt{n+1}-\sqrt{n})}{2n+1}\)
\(=\frac{2(\sqrt{n+1}-\sqrt{n})}{(n+1)+n}<\frac{2(\sqrt{n+1}-\sqrt{n})}{2\sqrt{n(n+1)}}\) (áp dụng bđt am-gm thì \((n+1)+n\geq 2\sqrt{n(n+1)}\), dấu bằng không xảy ra vì \(n\neq n+1\))
hay \(U_n< \frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\)
Do đó:
\(U_1+U_2+...+U_{2010}< \frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{3}}-...+\frac{1}{\sqrt{2010}}-\frac{1}{\sqrt{2011}}\)
\(\Leftrightarrow U_1+U_2+..+U_{2010}< 1-\frac{1}{\sqrt{2011}}< \frac{1005}{1006}\)
Ta có đpcm.

Dễ thấy \(u_n>0,\forall n\inℕ^∗\).
Ta có \(u_{n+1}-u_n=\dfrac{u_n^2+2021}{2u_n}-u_n=\dfrac{2021-u_n^2}{2u_n}\)
Với \(n\ge2\) thì \(u_n=\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\) \(=\dfrac{u_{n-1}}{2}+\dfrac{2021}{2u_{n-1}}\) \(>2\sqrt{\dfrac{u_{n-1}}{2}.\dfrac{2021}{2u_{n-1}}}\) \(=\sqrt{2021}\)
Vậy \(u_n>\sqrt{2021},\forall n\ge2\), suy ra \(u_{n+1}-u_n=\dfrac{2021-u_n^2}{2u_n}< 0,\forall n\inℕ^∗\)
\(\Rightarrow\) Dãy \(\left(u_n\right)\) là dãy giảm. Mà \(u_n>\sqrt{2021}\) \(\Rightarrow\left(u_n\right)\) có giới hạn hữu hạn. Đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L\) \(\Rightarrow L=\dfrac{L^2+2021}{2L}\) \(\Leftrightarrow L=\sqrt{2021}\)
Vậy \(\lim\limits_{n\rightarrow+\infty}u_n=\sqrt{2021}\)
Dễ thấy ��>0,∀�∈N∗un>0,∀n∈N∗.
Ta có ��+1−��=��2+20212��−��=2021−��22��un+1−un=2unun2+2021−un=2un2021−un2
Với �≥2n≥2 thì ��=��−12+20212��−1un=2un−1un−12+2021 =��−12+20212��−1=2un−1+2un−12021 >2��−12.20212��−1>22un−1.2un−12021 =2021=2021
Vậy ��>2021,∀�≥2un>2021,∀n≥2, suy ra ��+1−��=2021−��22��<0,∀�∈N∗un+1−un=2un2021−un2<0,∀n∈N∗
⇒⇒ Dãy (��)(un) là dãy giảm. Mà ��>2021un>2021 ⇒(��)⇒(un) có giới hạn hữu hạn. Đặt lim�→+∞��=�n→+∞limun=L ⇒�=�2+20212�⇒L=2LL2+2021 ⇔�=2021⇔L=2021
Vậy lim�→+∞��=2021n→+∞limun=2021

a. 5 số hạng đầu dãy là:
u1 = 2;
u2 = 2u1 – 1 = 3;
u3 = 2u2 – 1 = 5;
u4 = 2u3 – 1 = 9;
u5 = 2u4 – 1 = 17
b. Chứng minh un = 2n – 1 + 1 (1)
+ Với n = 1 ⇒ u1 = 21 - 1 + 1 = 2 (đúng).
+ Giả sử (1) đúng với n = k ≥ 1, tức là uk = 2k-1 + 1 (1)
Ta chứng minh: uk+1 = 2k + 1. Thật vậy, ta có:
⇒ uk+1 = 2.uk – 1 = 2(2k-1 + 1) – 1 = 2.2k – 1 + 2 – 1 = 2k + 1
⇒ (1) cũng đúng với n = k + 1 .
Vậy un = 2n – 1 + 1 với mọi n ∈ N.
\(u_1=1;u_2=4=2^2;u_3=9=3^2\)
Dự đoán: \(u_n=n^2\)
- Với \(n=1;2;3\) dãy đúng
- Giả sử \(u_k=k^2\)
- Ta cần chứng minh \(u_{k+1}=\left(k+1\right)^2\)
Thật vậy, ta có:
\(u_{k+1}=u_k+2k+1=k^2+2k+1=\left(k+1\right)^2\) (đpcm)