Một đĩa tròn đường kính 2m quay được 5 vòng trong 1 phút. Xác định chu kì, tần số, tốc độ góc, tốc độ dài và gia tốc hướng tâm của 1 điểm nằm ở mép đĩa.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
24 tháng 11 2021
1 phút = 60s
- Chu kì: T = \(\dfrac{t}{n}\)= \(\dfrac{60}{4}\)= 15 (s)
- Tần số: f = \(\dfrac{1}{T}\)=\(\dfrac{1}{15}\)(Hz)
- Tốc độ góc: T = \(\dfrac{2\pi}{\omega}\) \(\Rightarrow\) \(\omega=\dfrac{2\pi}{T}\)\(=\) \(\dfrac{2\pi}{15}=\dfrac{2}{15}\pi\) (rad/s)
- Tốc độ dài: \(\upsilon=r\omega\) ⇔ \(\upsilon=\dfrac{3}{2}.\dfrac{2}{15}\pi\) = \(\dfrac{1}{5}\pi\) (m/s)
- Gia tốc hướng tâm: \(a_{ht}=r.\omega^2\Leftrightarrow a_{ht}=\dfrac{3}{2}.\left(\dfrac{2}{15}\pi\right)^2\)\(\simeq\) 0,263 (m/\(s^2\))
vậy bài em làm như này sai òi hả🥲 cảm mơn
TK
12 tháng 10 2021
Đổi 30 cm =0,3 m; 1 phút =60s
a,\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{N}{t}}=\dfrac{1}{\dfrac{60}{60}}=1\left(s\right)\)
\(\omega=\dfrac{2\pi}{T}=2\pi\left(\dfrac{rad}{s}\right)\)
b,\(v=\dfrac{2\pi}{T}\cdot r=0,6\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,6\pi\right)^2}{0,3}=1,2\pi^2\left(\dfrac{m}{s^2}\right)\)
c, Đổi 10 cm =0,1m
Khoảng cách từ tâm đến điểm được xét =0,3-0,1=0,2(m)
<Rùi tính tiếp>
\(v'=\dfrac{2\pi}{T}r'=0,4\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}'=\dfrac{v'^2}{r'}=\dfrac{\left(0,4\pi\right)^2}{0,3}=\dfrac{8}{15}\pi^2\left(\dfrac{m}{s^2}\right)\)
TK
6 tháng 10 2021
Đổi 40 cm=0,4 m ; 1 phút =60s
Tốc độ dài của điểm A nằm trên vành đĩa
\(v=2\pi\cdot r\cdot f=2\pi\cdot r\cdot\dfrac{N}{t}=2\pi\cdot0,4\cdot\dfrac{30}{60}=0,4\pi\left(\dfrac{m}{s}\right)\)
Gia tốc hướng tâm của điểm A nằm trên vành đĩa
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,4\pi\right)^2}{0,4}=0,4\pi^2\left(\dfrac{m}{s^2}\right)\)
Tốc độ góc của của điểm A nằm trên vành đĩa
\(\omega=\dfrac{v}{r}=\dfrac{0,4\pi}{0,4}=\pi\left(\dfrac{rad}{s}\right)\)
VT
2 tháng 2 2018
Chọn đáp án C
+ Tốc độ góc: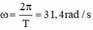 
+ Tốc độ dài: 
+ Gia tốc hướng tâm: 
VT
8 tháng 9 2017
Tốc độ góc của điểm A và điểm B bằng nhau: ω A = ω B
Tốc độ dài của điểm A và điểm B khác nhau:
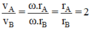
Gia tốc hướng tâm của điểm A và điểm B khác nhau:
VT
15 tháng 11 2017
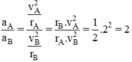
Tốc độ dài: v A = ω r A = 2 π T r A = 2.3 , 14 0 , 75 .0 , 37 = 3 , 1 m/s.
Tốc độ góc: v A = ω r A = 2 π T r A = 2.3 , 14 0 , 75 .0 , 37 = 3 , 1 rad/s.
Gia tốc hướng tâm: a A = v A 2 r A = 3 , 1 2 0 , 37 = 25 , 9 m / s 2 .
CT
12 tháng 10 2021
Đáp án:
Giải thích các bước giải:
a.
Chu kì là 0,8s
Tần số là:
Tần số góc là:
b.
Tốc độ dài của điểm A là:
c.
Tốc độ dài tại điểm đó là:
Tần số: \(f=5\)vòng/phút=\(\dfrac{1}{12}\)vòng/s
Chu kì chuyển động của vật: \(T=\dfrac{1}{f}=12s\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{12}=\dfrac{\pi}{6}\)(rad/s)
Tốc độ dài: \(v=\omega\cdot R=\dfrac{\pi}{6}\cdot1=\dfrac{\pi}{6}\approx0,52\)(m/s)
Gia tốc hướng tâm: \(a_{ht}=\dfrac{v^2}{R}=\dfrac{\left(\dfrac{\pi}{3}\right)^2}{1}=\dfrac{\pi^2}{9}\approx1,1\)m/s2
\(f=\dfrac{n}{t}=\dfrac{5}{60}=\dfrac{1}{12}\left(\dfrac{vong}{s}\right)\)
\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{1}{12}}=12\left(s\right)\)
\(\omega=2\pi f=2\pi\dfrac{1}{12}=\dfrac{1}{6}\pi\)
\(v=\omega R=\dfrac{1}{6}\pi\cdot2=\dfrac{1}{3}\pi\)
\(a_{huongtam}=\dfrac{v}{R}=\dfrac{\left(\dfrac{1}{3}\pi\right)^2}{1}\approx1,1\left(\dfrac{m}{s^2}\right)\)