Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét hình thang AHKB có
O là trung điểm của AB
OM//AHKB
Do đó: M là trung điểm của HK
b: Kẻ MN vuông góc với AB
Xét tứ giác AHMN có \(\widehat{AHM}+\widehat{ANM}=180^0\)
=>AHMN là tứ giác nội tiếp
=>\(\widehat{MAN}=\widehat{MHN}\)
Xét tứ giác MNBK có \(\widehat{MNB}+\widehat{MKB}=180^0\)
=>MNBK nội tiếp
=>\(\widehat{MBN}=\widehat{MKN}\)
Xét (O) có
ΔMAB nội tiếp
AB là đường kính
Do đó: ΔMAB vuông tại M
=>\(\widehat{MAB}+\widehat{MBA}=90^0\)
=>\(\widehat{NHK}+\widehat{NKH}=90^0\)
=>ΔNKH vuông tại N
ΔNKH vuông tại N có NM là trung tuyến
nên MH=MN
Xét (M) có
MN là bán kính
AB vuông góc MN tại N
Do đó: AB là tiếp tuyến của (M)
=>ĐPCM

a/
Ta có (M) tiếp xúc với AB tại H (gt) => AB là tiếp tuyến với (M)
Xét tg vuông ACM và tg vuông AHM có
AM chung
MC=MH (bán kính (M))
=> tg ACM = tg AHM (Hai tg vuông vó cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{AMC}=\widehat{AMH}\)
C/m tương tự khi xét 2 tg vuông BDM và BHM ta cũng có
\(\widehat{BMD}=\widehat{BMH}\)
Ta có
\(\widehat{AMH}+\widehat{BMH}=\widehat{AMB}=90^o\) (góc nt chắn nửa đường tròn)
\(\Rightarrow\widehat{AMC}+\widehat{BMD}=\widehat{AMH}+\widehat{BMH}=\widehat{AMB}=90^o\)
\(\Rightarrow\widehat{AMC}+\widehat{BMD}+\widehat{AMB}=90^o+90^o=180^o=\widehat{CMD}\)
=> C; M; D thẳng hàng
Ta có
\(AC\perp CD;BD\perp CD\) => AC//BD
b/ Ta có
AC//BD (cmt) => ACDB là hình thang
Mà
MC=MD (bán kính (M)
OA=OB=R
=> OM là đường trung bình của hình thang ACDB => OM//BD
Mà \(BD\perp CD\)
\(\Rightarrow OM\perp CD\) => CD là tiếp tuyến với (O)
c/
Ta có
AC=AH (2 tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn)
BD=BH (2 tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn)
\(\Rightarrow AC+BD=AH+BH=AB=2R\) không đổi
d/
Khi HC=HD => tg AHD cân tại H
Ta có MC=MD
\(\Rightarrow MH\perp CD\) (trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao)
Mà \(OM\perp CD\left(cmt\right)\)
\(\Rightarrow H\equiv O\)
Xét tg AMB có
\(MH\perp AB\Rightarrow MO\perp AB\)
Mà OA=OB
=> tg AMB cân tại M (tam giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
=> MA=MB => sđ cung MA = sđ cung MB (trong đường tròn 2 dây cung bằng nhau thì số đo 2 cung tương ứng bằng nhau)
=> M là điểm giưa cung AB

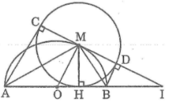
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = AH và BD = BH
Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH
Suy ra: AC + BD = AH + BH = AB không đổi

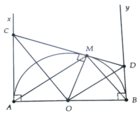
a, HS tự chứng minh
b, ΔCOD và ΔAMB đồng dạng => MC.MD = O M 2
c, AC = R 3
BD.AC = MC.MD = O M 2
=> BD = R 3 3
Hướng dẫn, ghét hình học phẳng:
Để ý rằng AB vuông góc (M) tại H nên AH, BH cũng là các tiếp tuyến của (M)
- Nối MA, MB
- \(\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn (O) nên suy ra...
- AH, AC là 2 tiếp tuyến \(\Rightarrow\widehat{AMC}=\widehat{AMH}\)
Tương tự: \(\widehat{BMD}=\widehat{BMH}\)
\(\Rightarrow\widehat{CMD}=2\left(\widehat{AMH}+\widehat{BMH}\right)\)
b. AC, AH, BD, BH là các tiếp tuyến nên \(\left\{{}\begin{matrix}AC=AH\\BD=BH\end{matrix}\right.\) \(\Rightarrow AC+BD=...\)
c.
AC song song BD (cùng vuông CD), O và M lần lượt là trung điểm AB, CD
\(\Rightarrow OM\) là đtb hình thang vuông ABDC \(\Rightarrow OM\) vuông CD
Hệ thức lượng tam giác vuông OMK: \(OM^2=OH.OK\)
Mà \(OM=\dfrac{AB}{2}\Rightarrow...\)