Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔASC có
O,E lần lượt là trung điểm của AC,AS
=>OE là đường trung bình của ΔASC
=>OE//SC
OE//SC
\(SC\subset\left(SCD\right)\)
OE không nằm trong mp(SCD)
Do đó: OE//(SCD)
b: Xét ΔBSD có
O,F lần lượt là trung điểm của BD,BS
=>OF là đường trung bình của ΔBSD
=>OF//SD
OF//SD
SD\(\subset\left(SCD\right)\)
OF không nằm trong (SCD)
Do đó: OF//(SCD)
c: OF//(SCD)
OE//(SCD)
OF,OE cùng thuộc mp(OEF)
Do đó: (OEF)//(SCD)

Đáp án A
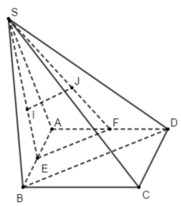
Tam giác SAB có I là trọng tâm và E là trung điểm của AB
Nên ta có S I S E = 2 3 (1)
Tam giác SAD có J là trọng tâm và F là trung điểm của AD
Nên ta có S J S F = 2 3 (2)
Từ (1) và (2) ta có: IJ // EF (3) (định lý Ta-lét trong tam giác SEF)
Tam giác ABD có EF là đường trung bình nên EF // BD (4)
Từ (3) và (4) suy ra IJ // BD
Mà BD (SBD)
Do đó IJ // (SBD).

Đáp án C
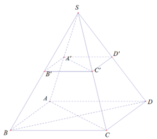
A’B’ // AB ( A’, B’ lần lượt là trung điểm SA, SB)
B’C’ // BC (B’, C’ lần lượt là trung điểm SB, SC)
Mà A’B’ và B’C’ cắt nhau; AB và BC cắt nhau.
⇒ (A’B’C’D’) // (ABCD)
⇒ (A’C’D’) // (ABC)

a: ABCD là hình chữ nhật tâm O
=>O là trung điểm chung của AC và BD
Xét ΔASC có
O,E lần lượt là trung điểm của AC,AS
=>OE là đường trung bình
=>OE//SC
mà SC\(\subset\left(SCD\right)\) và OE không thuộc (SCD)
nên OE//(SCD)
b: Xét ΔBSD có
\(\dfrac{BO}{BD}=\dfrac{BF}{BS}=\dfrac{1}{2}\)
nên OF//SD
=>OF//(SDC)
c: OE//(SDC)
OF//(SDC)
\(OE,OF\subset\left(OEF\right)\)
Do đó: (OEF)//(SCD)

Qua S kẻ đường thẳng d song song AD (và BC)
Do \(\left\{{}\begin{matrix}S\in\left(SAD\right)\cap\left(SBC\right)\\AD||BC\\AD\in\left(SAD\right)\\BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\) giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song AD, BC
\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)
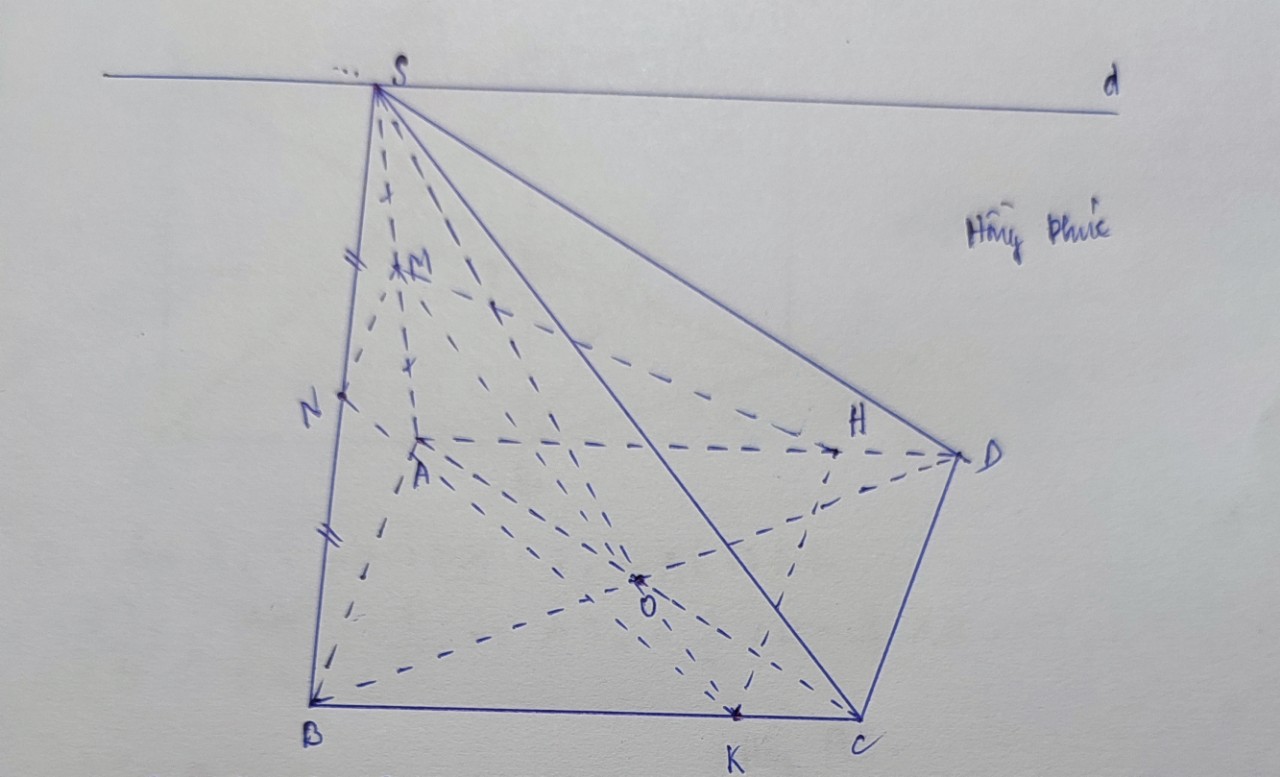
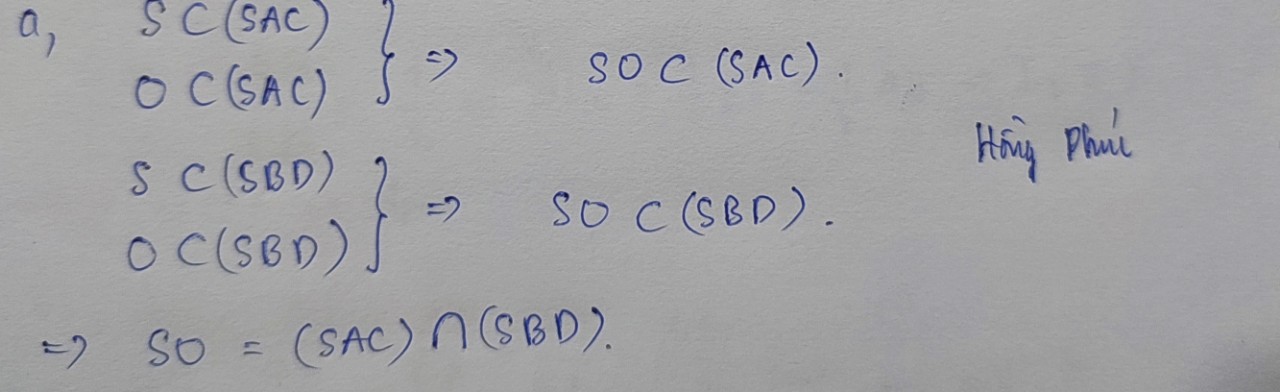
Ta có: OF là đường trung bình tam giác SAC
\(\Rightarrow OF//SA\Rightarrow OF//\left(SAD\right)\)
OE là đường trung bình tam giác SBD
\(\Rightarrow OE//SD\Rightarrow OE//\left(SAD\right)\)
\(\Rightarrow\left(OEF\right)//\left(SAD\right)\)
Cảm ơn bạn