Cho hình vuông ABCD có cạnh bằng a và có diện tích bằng S1. Nói 4 trung điểm mỗi cạnh ta được hình vương với diện tích S2. Cứ làm như thế khi có 20 hình. tính tống S=S1+S2....+S20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
Phương pháp:
Nếu u n là một cấp số nhân với công bội q ≠ 1 thì S n được tính theo công thức: S n = u 1 1 − q n 1 − q .
Cách giải:
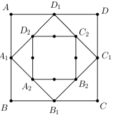
Hình vuông ABCD cạnh a ⇒ S 1 = a 2
Hình vuông A 1 B 1 C 1 D 1 có cạnh bằng a 2 ⇒ S 2 = a 2 2
Hình vuông A 2 B 2 C 2 D 2 có cạnh bằng
a 2 2 = a 2 2 ⇒ S 3 = a 2 2 2
……
Hình vuông A 99 B 99 C 99 D 99 có cạnh bằng a 2 99 ⇒ S 100 = a 2 2 99
S = S 1 + S 2 + S 3 + ... + S 100 = a 2 2 0 + a 2 2 1 + a 2 2 2 + ... + a 2 2 99 = a 2 . 1 − 1 2 100 1 − 1 2 = a 2 2 100 − 1 2 100 .2 = a 2 2 100 − 1 2 99

Ta tính được
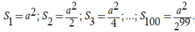
Như vậy
S
1
,
S
2
,
S
3
,
.
.
.
,
S
100
là cấp số nhân với ![]()
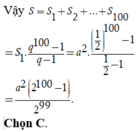

Đáp án C
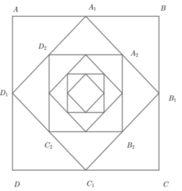
Diện tích hình vuông A B C D là S 1 = a 2 ; diện tích hình vuông A 1 B 1 C 1 D 1 là S 2 = a 2 2 2 = a 2 2
Diện tích hình vuông A 2 B 2 C 2 D 2 là a 2 2 = a 2 4 ; ...
Diện tích hình vuông A 99 B 99 C 99 D 99 là S 100 = a 2 2 99
Vậy S = a 2 1 2 0 + 1 2 1 + 1 2 2 + ... + 1 2 99 ⏟ T
với T là tổng của CSN có u 1 = 1 ; q = 1 2 và n = 100
Do đó, tổng:
S = a 2 . 1 − 1 2 100 1 − 1 2 = 2 a 2 1 − 1 2 100 = a 2 2 100 − 1 2 99

Chọn D.
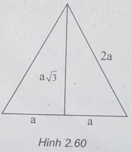
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.
Do đó, ta có:
S 1 = π Rl = π .a.2a = 2 πa 2 (1)
Mặt cầu có bán kính là a 3 /2, nên ta có:
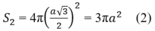
Từ (1) và (2) suy ra: 2 S 2 = 3 S 1





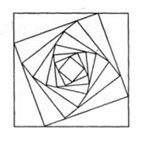
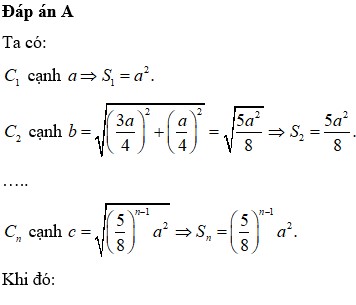

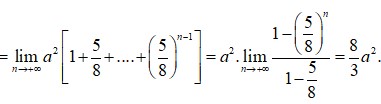
Gọi cạnh của hình vuông có diện tích \(S_k\) là \(a_k\) thì \(a_{k+1}=\dfrac{a_k}{\sqrt{2}}\)
\(\Rightarrow S_{k+1}=\dfrac{1}{2}S_k\)
Do đó:
\(S=S_1+\dfrac{1}{2}S_1+...+\dfrac{1}{2^{19}}S_1\)
\(=a^2\left(1+\dfrac{1}{2}+...+\dfrac{1}{2^{19}}\right)=a^2\left(2-\dfrac{1}{2^{19}}\right)\)