tìm số hạng chứa x\(^{15}\) trong khai triển : (2x\(^3\) - \(\dfrac{1}{4x^2}\))\(^{40}\) (x\(\ne\)0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


SHTQ là: \(C^k_5\cdot\left(x^3\right)^{5-k}\cdot\left(\dfrac{1}{x}\right)^k=C^k_5\cdot x^{15-4k}\)
Số hạng chứa x^3 tương ứng với 15-4k=3
=>4k=12
=>k=3
=>Hệ số là \(C^3_5=10\)
Để tìm hệ số của số hạng chứa x3 trong khai triển ( x 3 + 1 x ) 5 , ta sử dụng công thức tổng hạng:
Tổng hạng = ∑ C(n, k)
Trong đó:
C(n, k) là số cấu hình có k phần tử trong tổng hạng nn là số lượng phần tử trong tổng hạngk là số lượng phần tử không chứa xVì ta chỉ quan tâm đến số hạng chứa x3, nên không quan tâm đến số lượng phần tử trong tổng hạng n.
Số hạng chứa x3 trong khai triển ( x 3 + 1 x ) 5 (với x ≠ 0) là 2.
Hệ số của số hạng chứa x3 trong khai triển ( x 3 + 1 x ) 5 (với x ≠ 0) là 2/3.

Chắc là thế này \(3A^{n-2}_n\)
\(gt\Leftrightarrow2.n!-\left(4n+5\right)\left(n-2\right)!=3.\dfrac{n!}{2!}\)
\(\Leftrightarrow\dfrac{1}{2}n!=\left(4n+5\right)\left(n-2\right)!\Leftrightarrow\dfrac{1}{2}n\left(n-1\right)\left(n-2\right)!=\left(4n+5\right)\left(n-2\right)!\)
\(\Leftrightarrow\dfrac{1}{2}n\left(n-1\right)=4n+5\Leftrightarrow n=10\)
\(\left(3x^3-\dfrac{1}{x^2}\right)^{10}=\left(3x^3-x^{-2}\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}3^{10-k}.x^{3\left(10-k\right)}.\left(-1\right)^k.x^{-2k}\)
\(=\sum\limits^{10}_{k=0}C^k_{10}.\left(-1\right)^k.3^{10-k}.x^{30-5k}\)
=> so hang ko chua x: \(30-5k=0\Leftrightarrow k=6\)
\(\Rightarrow C^6_{10}.\left(-1\right)^6.3^{10-6}=17010\)


\(C^1_n+C^2_n=15\) (Điều kiện: \(n\ge2\))
\(\Leftrightarrow n+\dfrac{n!}{2!\left(n-2\right)!}=15\)
\(\Leftrightarrow n+\dfrac{n\left(n-1\right)\left(n-2\right)!}{2\left(n-2\right)!}=15\)
\(\Leftrightarrow n+\dfrac{n\left(n-1\right)}{2}=15\)
\(\Leftrightarrow2n+n\left(n-1\right)=30\)
\(\Leftrightarrow2n+n^2-n=30\)
\(\Leftrightarrow n^2+n-30=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=5\\n=-6\left(\text{loại}\right)\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{2}{x^4}\right)^5=C^k_5x^{5-k}\left(\dfrac{2}{x^4}\right)^k=C^k_5x^{5-k-4k}.2^k=C^k_5x^{5-5k}.2^k\)
\(ycbt\Leftrightarrow5-5k=0\Leftrightarrow k=1\)
\(\Rightarrow C^1_5.2^1=10\)
Vậy số hạng không chứa \(x\) trong khai triển là \(10\).

Chọn C.
Ta có 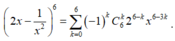 .
.
Số hạng thứ k + 1 là ![]() .
.
Tìm số hạng không chứa x trong khai triển khi: 6 - 3k = 0 => k = 2
Với k = 2 ta có số hạng không chứa x là: ![]() .
.

Số hạng tổng quát trong khai triển:
\(C_{10}^k.\left(2x^3\right)^k.\left(x^{-2}\right)^{10-k}=C_{10}^k.2^k.x^{3k}.x^{2k-20}=C_{10}^k.2^k.x^{5k-20}\)
Số hạng không chứa x \(\Rightarrow5k-20=0\Rightarrow k=4\)
Số hạng đó là: \(C_{10}^4.2^4=...\)


Khai triển \(\left(2x^3-\dfrac{1}{4}x^{-2}\right)^{40}\) có số hạng tổng quát:
\(C_{40}^k\left(2x^3\right)^k\left(\dfrac{1}{4}\right)^{40-k}.\left(x^{-2}\right)^{40-k}=C_{40}^k2^k.4^{k-40}.x^{5k-80}\)
Số hạng chứa\(x^{15}\Rightarrow5k-80=15\Leftrightarrow k=19\)
Số hạng đó là: \(C_{40}^{19}2^{19}.4^{-21}x^{15}=C_{40}^{19}.\dfrac{1}{2^{23}}.x^{15}\)