K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
21 tháng 2 2022
vs đk tổng =1 ta có:
\(\dfrac{a+bc}{b+c}+\dfrac{b+ca}{c+a}+\dfrac{c+ab}{a+b}\)
\(=\dfrac{a\left(a+b+c\right)+bc}{bc}+\dfrac{b\left(a+b+c\right)+ca}{ca}+\dfrac{c\left(a+b+c\right)+ab}{ab}\)
\(=\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(b+c\right)\left(b+a\right)}{c+a}+\dfrac{\left(c+a\right)\left(c+b\right)}{a+b}\)
sd bđt AM-GM cho 2 số dương ta có:
\(\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(b+c\right)\left(b+a\right)}{c+a}\ge2\left(a+b\right)\)
\(\dfrac{\left(b+c\right)\left(b+a\right)}{c+a}+\dfrac{\left(c+a\right)\left(c+b\right)}{a+b}\ge2\left(b+c\right)\)
\(\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(c+a\right)\left(c+b\right)}{a+b}\ge2\left(c+a\right)\)
Cộng theo vế 3 đẳng thức trên ta sẽ có điều phải chứng minh
Đẳng thức xảy ra khi và chỉ khi a = b= c =\(\dfrac{1}{3}\)
NN
1
22 tháng 8 2021
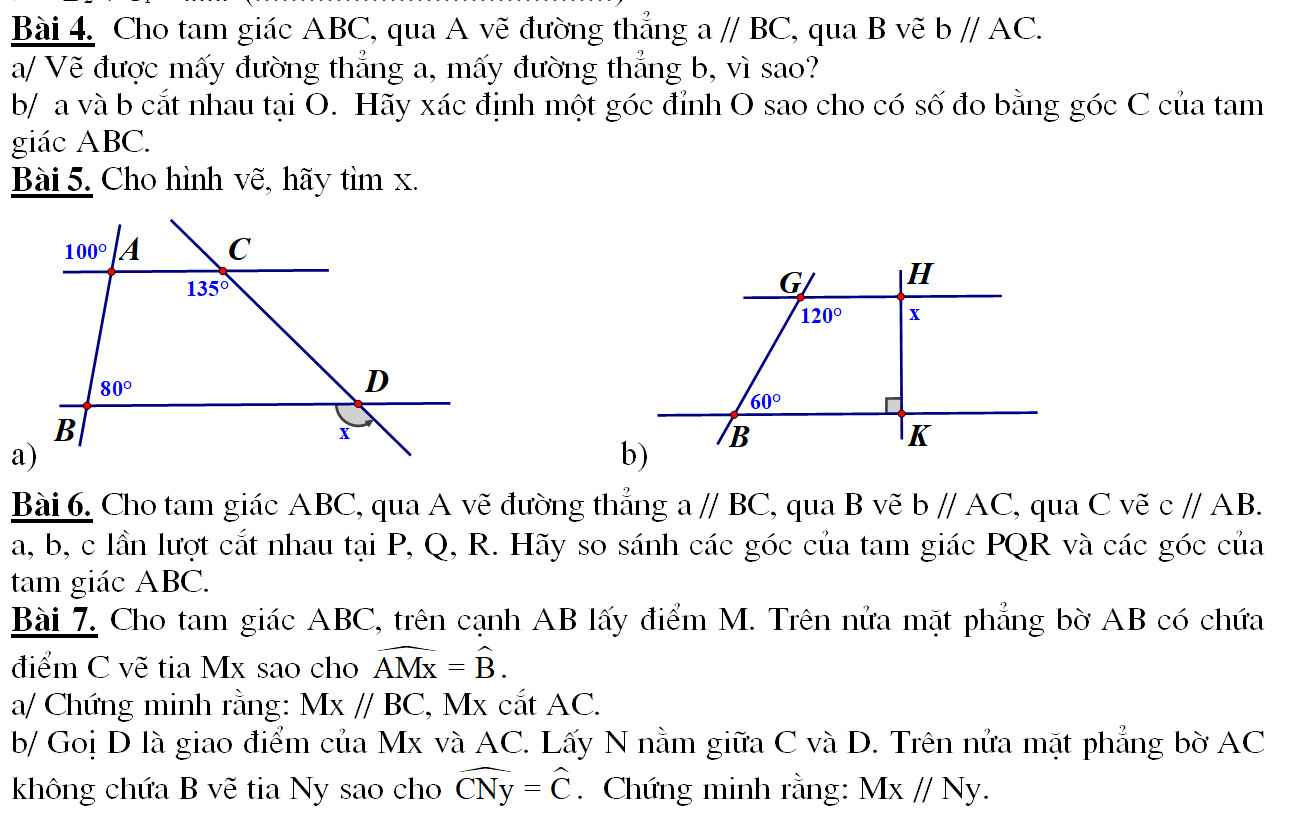
a) x = 135 (2 góc đồng vi)
b) x = 90 vì góc K và góc H là 2 góc trong cùng phía, tính chất của 2 góc trong cùng phía là bù nhau nên ta có: 180 - 90 = 90
LT
3
AH
Akai Haruma
Giáo viên
28 tháng 1 2023
Bài 6:
Hiệu số tuổi 2 anh em: $10-5=5$ (tuổi)
Khi tuổi em bằng 2/3 tuổi anh thì tuổi em là:
$5:(3-2)\times 2=10$ (tuổi)
Vậy tuổi em bằng 2/3 tuổi anh sau:
$10-5=5$ (năm)
AH
Akai Haruma
Giáo viên
28 tháng 1 2023
Bài 7:
Gọi số học sinh tham gia giao lưu là $x$.
Tổng số cuốn vở là: $9\times x+80$
Tổng số cuốn vở cũng bằng: $11\times x-80$
Vậy: $9\times x+80=11\times x-80$
$80+80=11\times x-9\times x$
$160=x\times (11-9)=x\times 2$
$x=160:2=80$
Vậy có 80 bạn tham gia giao lưu.
HM
0
NV
1
19 tháng 7 2017
\(3x^2+30x=6000\Leftrightarrow x^2+10x=2000\Leftrightarrow x^2+10x-2000=0\)
\(\Leftrightarrow x^2-40x+50x-2000=0\Leftrightarrow x\left(x-40\right)+50\left(x-40\right)=0\)
\(\Leftrightarrow\left(x+50\right)\left(x-40\right)=0\Leftrightarrow\left\{{}\begin{matrix}x+50=0\\x-40=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-50\\x=40\end{matrix}\right.\)
vậy phương trình có 2 nghiệm phân biệt \(x=40;x=-50\)