Nếu x < 0 , y < 0 thì căn bậc hai của xy có phải không xác định hay không ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn chỉ cần hiểu là căn bậc hai số học của là một số x sao cho \(x^2=a\) và \(x\ge0\) thôi

Không phải là căn bậc hai số học là đứng độc lập 1 mình đâu bạn
Những trường hợp em nêu đều là CBHSH
$2\sqrt{3}$ là căn bậc 2 số học của $12$
$\sqrt{3}.\sqrt{4}$ là căn bậc 2 số học của $12$
$\sqrt{\frac{3}{4}}$ là căn bậc 2 số học $\frac{3}{4}$
Em cứ nhớ $\sqrt{x}$ (với $x$ là số không âm) là CBHSH của $x$, dù nó biểu diễn kiểu gì đi chăng nữa.

\(y=-\dfrac{1}{2}x\) là hàm số bậc nhất
Với: \(a=-\dfrac{1}{2};b=0\)

a) \({x^2} + x - 6 \le 0\) là một bất phương trình bậc hai một ẩn
Vì \({2^2} + 2 - 6 = 0\) nên \(x = 2\) là nghiệm của bất phương trình trên
b) \(x + 2 > 0\) không là bất phương trình bậc hai một ẩn
c) \( - 6{x^2} - 7x + 5 > 0\) là một bất phương trình bậc hai một ẩn
Vì \( - {6.2^2} - 7.2 + 5 = - 33 < 0\) nên \(x = 2\) không là nghiệm của bất phương trình trên

ĐK: `-x^4-2 >=0 <=>-(x^4+2) >=0 <=> x^4+2 <=0`
`x^4 >=0 <=>x^4+2>=2 >0 forallx`
Là "`-x^4`" chứ không phải "`(-x)^4`" ạ.

1:
uses crt;
var a,b:real;
begin
clrscr;
write('Nhap a='); readln(a);
write('Nhap b='); readln(b);
if a<>0 then writeln('Nghiem cua phuong trinh la: ',-b/a:4:2)
else writeln('Phuong trinh vo nghiem');
readln;
end.
2:
uses crt;
var n:real;
begin
clrscr;
write('Nhap n='); readln(n);
if n>=0 then writeln('Can bac hai cua n la: ',trunc(sqrt(n)))
else writeln(n,' khong co can bac hai');
readln;
end.
3:
uses crt;
var a,b,c:real;
begin
clrscr;
repeat
write('Nhap a='); readln(a);
write('Nhap b='); readln(b);
write('Nhap c='); readln(c);
until (a>0) and (b>0) and (c>0);
if (a+b>c) and (a+c>b) and (b+c>a) then writeln('Day la do dai ba canh trong mot tam giac')
else writeln('Day khong la do dai ba canh trong mot tam giac');
readln;
end.

y=x-1 mới là hàm số bậc nhất chứ x-1 không phải hàm số mà chỉ là biểu thức thôi nha bạn

a) Ta có \((x - 1)(2 - 3x) = 2x - 3{x^2} - 2 + 3x = - 3{x^2} + 5x - 2\)
Do đó hàm y=(x-1)(2-3x) là hàm số bậc hai với \(a = - 3;b = 5;c = - 2\)
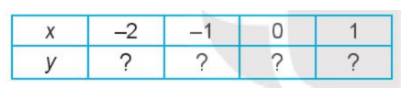
b) Thay các giá trị của x vào y = (x - 1)(2 - 3x) ta có:

\(\sqrt{xy}\)vẫn xác định khi \(x< 0;y< 0\)(khi đó \(xy>0\)), nhưng đừng bao giờ viết \(\sqrt{xy}=\sqrt{x}.\sqrt{y}\)
có xác định