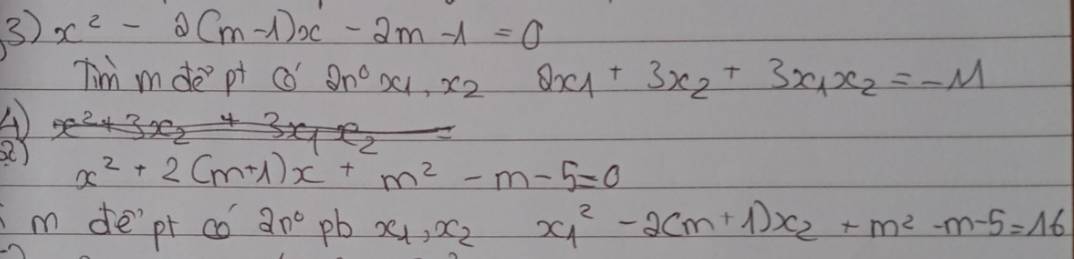Giải giúp mình bài 1,2,3 với
Giải giúp mình bài 1,2,3 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8


1:
a: A=x^4+6x^3-3x^2-4x+8
bậc là 4
B=-x^4-6x^3+3x^2-2x+5
bậc là 4
b: A(x)+B(x)
=x^4+6x^3-3x^2-4x+8-x^4-6x^3+3x^2-2x+5
=-6x+13
A(x)-B(x)
=x^4+6x^3-3x^2-4x+8+x^4+6x^3-3x^2+2x-5
=2x^4+12x^3-6x^2-2x+3




3.
\(\Delta'=\left(m-1\right)^2-\left(-2m-1\right)=m^2+2>0;\forall m\)
\(\Rightarrow\) Pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-2m-1\end{matrix}\right.\)
\(2x_1+3x_2+3x_1x_2=-11\)
\(\Leftrightarrow2\left(x_1+x_2\right)+x_2+3x_1x_2=-11\)
\(\Leftrightarrow4\left(m-1\right)+x_2+3\left(-2m-1\right)=-11\)
\(\Leftrightarrow x_2=2m-4\)
Thế vào \(x_1+x_2=2\left(m-1\right)\)
\(\Rightarrow x_1=2\left(m-1\right)-\left(2m-4\right)=2\)
Thế \(x_1=2;x_2=2m-4\) vào \(x_1x_2=-2m-1\)
\(\Rightarrow2\left(2m-4\right)=-2m-1\)
\(\Rightarrow m=\dfrac{7}{6}\)
4.
\(\Delta'=\left(m+1\right)^2-\left(m^2-m-5\right)=3m+6>0\Rightarrow m>-2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2\left(m+1\right)\\x_1x_2=m^2-m-5\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên:
\(x_1^2+2\left(m+1\right)x_1+m^2-m-5=0\)
\(\Rightarrow x_1^2=-2\left(m+1\right)x_1-m^2+m+5\)
Từ đó ta được:
\(x_1^2-2\left(m+1\right)x_2+m^2-m-5=16\)
\(\Leftrightarrow-2\left(m+1\right)x_1-m^2+m-5-2\left(m+1\right)x_2+m^2-m-5=16\)
\(\Leftrightarrow-2\left(m+1\right)\left(x_1+x_2\right)=16\)
\(\Leftrightarrow4\left(m+1\right)^2=16\)
\(\Leftrightarrow\left(m+1\right)^2=4\)
\(\Rightarrow\left[{}\begin{matrix}m+1=2\\m+1=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=1\\m=-3< -2\left(loại\right)\end{matrix}\right.\)



 Đây anh
Đây anh