
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(=\dfrac{2^{15}\cdot3^8}{3^6\cdot2^6\cdot2^9}+\dfrac{9^3\cdot71}{3^2\cdot71}=3^2+81=90\)

\(=\dfrac{2^4\cdot5^4\cdot3^6}{2^8\cdot3^4}=3^2\cdot5^4\cdot\dfrac{1}{2^4}\)

a, M(x)= 3x^3 - 2x^2 + 1 (đã rút gọn ) , ý b bạn chỉ cần thay M(-1) và M(2) vào x lần lượt từng con là đc vd : M(-1)= 3* (-1^3) - 2* (- 1)^2 + 1 rồi tính ra kết quả là được

2:
căn c+25=34
=>căn c=9
=>c=81
=>c^2-28=81^2-28=6533
3: xy-3x+y=14
=>x(y-3)+y-3=11
=>(y-3)(x+1)=11
=>(x+1;y-3) thuộc {(1;11); (11;1); (-1;-11); (-11;-1)}
=>(x,y) thuộc {(0;14); (10;4); (-2;-8); (-12;2)}
4:
TH1: AC=5cm
AB+AC<BC
=>Loại
TH2: AC=11cm
BC+AC>AB; BC+AB>AC; AB+AC>BC
=>Nhận
C ABC=11+11+5=27(cm)



Câu 4:
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)

Câu 15:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
DO đó: ΔADF=ΔEDC
Suy ra: DF=DC
c: Ta có: ΔBFC cân tại B
mà BD là phân giác
nên BD là đường cao





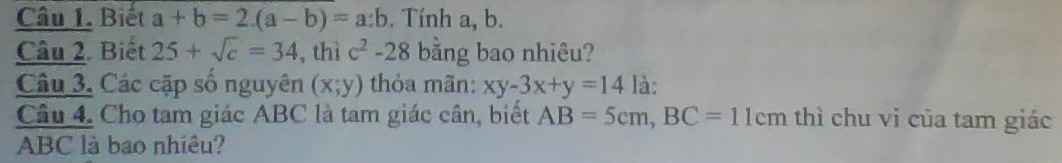



1:
a: A=x^4+6x^3-3x^2-4x+8
bậc là 4
B=-x^4-6x^3+3x^2-2x+5
bậc là 4
b: A(x)+B(x)
=x^4+6x^3-3x^2-4x+8-x^4-6x^3+3x^2-2x+5
=-6x+13
A(x)-B(x)
=x^4+6x^3-3x^2-4x+8+x^4+6x^3-3x^2+2x-5
=2x^4+12x^3-6x^2-2x+3