Tìm giá trị nhỏ nhất của biểu thức: x 2 + x 3 + 1 . Giá trị đó đạt được khi x bằng bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
17 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
30 tháng 7 2015
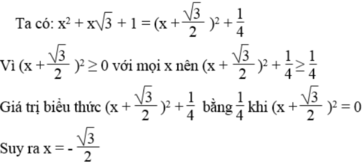
\(=x^2+2.x\cdot\frac{\sqrt{3}}{2}+\frac{3}{4}+\frac{1}{4}=\left(x+\frac{\sqrt{3}}{4}\right)^2+\frac{1}{4}\)
Vậy GTNN là 1/4 khi \(x+\frac{\sqrt{3}}{2}=0\Rightarrow x=-\frac{\sqrt{3}}{2}\)
3 tháng 2 2022
a: \(P=\dfrac{x+\sqrt{x}+1+11\sqrt{x}-11+34}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x+\sqrt{x}+1-x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x+12\sqrt{x}+24}{\sqrt{x}+2}\)
b: Thay \(x=3-2\sqrt{2}\) vào P, ta được:
\(P=\dfrac{3-2\sqrt{2}+12\left(\sqrt{2}-1\right)+24}{\sqrt{2}-1+2}\)
\(=\dfrac{27-2\sqrt{2}+12\sqrt{2}-12}{\sqrt{2}+1}=5+5\sqrt{2}\)
31 tháng 7 2016
\(A=\sqrt{x^2+2x+1}+\sqrt{x^2-2x+1}\)
\(=\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-1\right)^2}\)
-Nêú \(x\ge1\)thì \(\sqrt{\left(x+1\right)^2}=x+1\)và\(\sqrt{\left(x-1\right)^2}=x-1\)
Ta có:\(A=x+1+x-1=2x\ge2\)
Dấu "=" xảy ra khi x=1
-Nếu\(1>x\ge-1\)thì \(\sqrt{\left(x+1\right)^2}=x+1\)và\(\sqrt{\left(x-1\right)^2}=1-x\)
Ta có:\(A=x+1+1-x=2\)
-Nếu x<-1 thì \(\sqrt{\left(x+1\right)^2}=-x-1\)và\(\sqrt{\left(x-1\right)^2}=1-x\)
Ta có:\(A=-x-1+1-x=-2x\ge2\)
Dấu "=" xảy ra khi x=-1
Vậy GTNN của A là 2 tại x=1 hoặc x=-1
6 tháng 11 2016
bài 2
Ta có:
\(A=\left|x-102\right|+\left|2-x\right|\Rightarrow A\ge\left|x-102+2-x\right|=-100\Rightarrow GTNNcủaAlà-100\)đạt được khi \(\left|x-102\right|.\left|2-x\right|=0\)
Trường hợp 1: \(x-102>0\Rightarrow x>102\)
\(2-x>0\Rightarrow x< 2\)
\(\Rightarrow102< x< 2\left(loại\right)\)
Trường hợp 2:\(x-102< 0\Rightarrow x< 102\)
\(2-x< 0\Rightarrow x>2\)
\(\Rightarrow2< x< 102\left(nhận\right)\)
Vậy GTNN của A là -100 đạt được khi 2<x<102.
29 tháng 10 2023
ĐKXĐ: x>=4
\(A=\dfrac{1}{x-4\sqrt{x-4}+3}\)
\(=\dfrac{1}{x-4-4\sqrt{x-4}+4+3}\)
\(=\dfrac{1}{\left(\sqrt{x-4}-2\right)^2+3}\)
\(\left(\sqrt{x-4}-2\right)^2+3>=3\)
=>\(A=\dfrac{1}{\left(\sqrt{x-4}-2\right)^2+3}< =\dfrac{1}{3}\)
Dấu = xảy ra khi \(\sqrt{x-4}-2=0\)
=>x-4=4
=>x=8