cho mình hỏi câu này
cho (d):
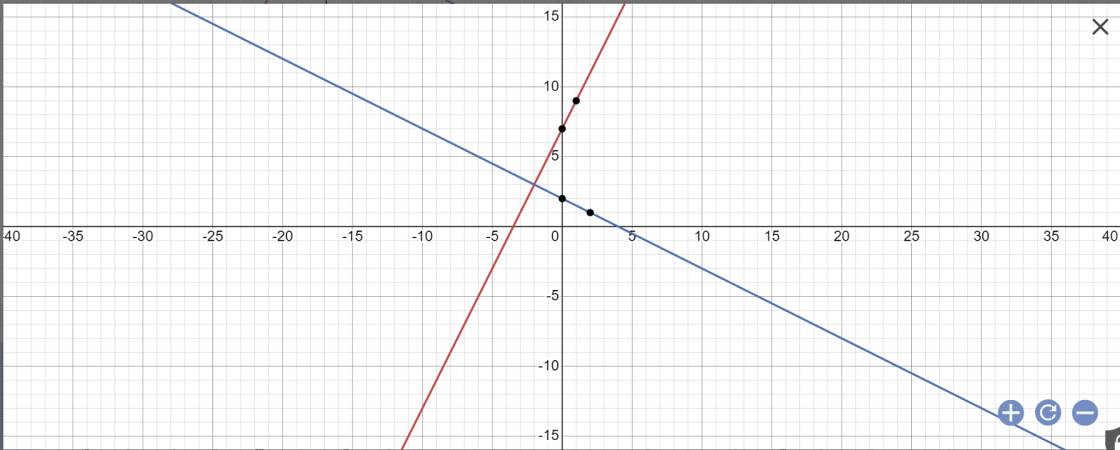
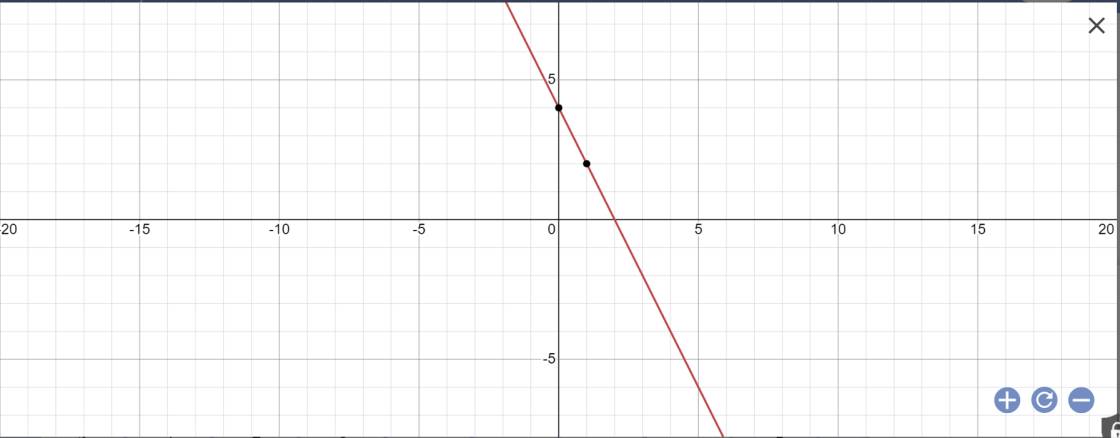
1) với m = -3 : a) vẽ đồ thị h/số trên b) tìm tọa độ giao điểm của (d) với (d2) : y = 2x - 1 c) gọi A,B lần lượt là giao của (d) với Ox,Oy . tính Soab d) tính k/c từ 0 đến (d)
2) tìm m biết đồ thị h//số (d) đi qua điểm M (1,2)
3) tìm m biết đồ thị h/số (d) cắt trục trung tại điểm có trung độ bằng 1
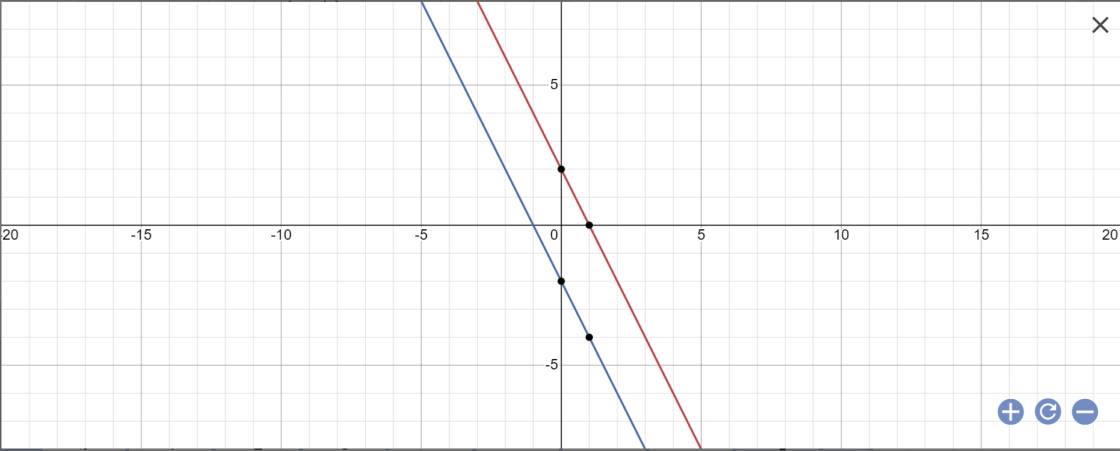
4) cho (d2) : y = x + 5 ; (d3) : y = -x - 2 tìm m để 3 đường thẳng (d),(d2),(d3) đồng quy