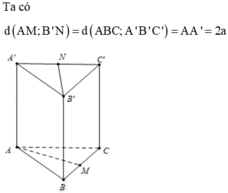
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh bằng a và chiều cao bằng 2a. Gọi M, N lần lượt là trung điểm của BC và A’C’
A. 2a
B. a 3
C. a
D. a 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 8 2017
Đáp án B.
Dễ thấy:
A B ' C ' ; M N P ^ = A B ' C ' ; M N C B ^
= 180 0 − A B ' C ' ; A ' B ' C ' ^ − M N B C ; A ' B ' C ' ^ = 180 0 − A ' B C ; A B C ^ − M N B C ; A B C . ^
Ta có:
M N B C ; A B C ^ = A ' P ; A P ^ = A ' P A ^ = arctan 2 3 .
Và
M N B C ; A B C ^ = S P ; A P ^ = S P A ^ = arctan 4 3 ,
với S là điểm đối xứng với A qua A’,
thì S A = 2 A A ' = 4.
Suy ra
cos A B ' C ' ; M N P ^ = c os 180 0 -arctan 2 3 − arctan 4 3 = 13 65 .
CM
15 tháng 1 2017
Đáp án B.
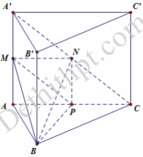
Ta có B P ⊥ A C B P ⊥ A ' A ⇒ B P ⊥ A ' A C ⇒ B P ⊥ M N P
Ta có M N = 1 2 A C = a ; N P = 1 2 A ' A = 3 a 2
⇒ S M N P = 1 2 M N . N P = 3 a 2 4
Ta có B P = 2 a 3 2 = a 3
V B . M N P = 1 3 B P . S M N P = 1 3 . a 3 . 3 a 2 4 = a 3 3 4 .
Đáp án là A
