Gía trị lớn nhất của hàm số y = x 3 − 2 x 2 − 4 x + 5 trên đoạn [1;3] bằng
A. -3
B. 0
C. 2
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án là A .
Ta có:
• y ' = 6 x 2 + 6 x − 12 , cho y ' = 0 ⇔ x = − 2 ∉ − 1 ; 2 x = 1 ∈ − 1 ; 2 .
• y − 1 = 15 ; y 2 = 6 ; y 1 = − 5.
Vậy x 0 = 1.

Đáp án là B
Đáy hình thoi cạnh a, góc B C A ^ = 30 0 ⇒ B C D ^ = 60 0
Nên suy ra B D = a , A C = 2. O C = 2. a 3 2 = a 3
Vậy diện tích đáy d t A B C D = 1 2 A C . B D = 1 2 . a 3 . a = a 2 3 2
Vậy thể tích V = 1 3 S O . d t A B C D = a 3 3 8

TXĐ: D = (-∞; 1) ∪ (1; +∞)
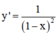 > 0 với ∀ x ∈ D.
> 0 với ∀ x ∈ D.
⇒ hàm số đồng biến trên (-∞; 1) và (1; +∞).
⇒ Hàm số đồng biến trên [2; 4] và [-3; -2]
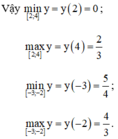

Đáp án là D.
• Ta có: y , = - 1 - 1 ( 2 + x ) 2 cho y , = 0 ⇔ x = - 1 x = - 3
• Bảng biến thiên:
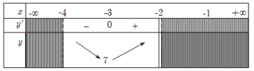
Từ BBT ta có: m i n - 4 ; - 2 y = 7

\(y'=3x^2-6x-9=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
a. Trên [-4;4] ta có:
\(y\left(-4\right)=-41\) ; \(y\left(-1\right)=40\) ; \(y\left(3\right)=8\) ; \(y\left(4\right)=15\)
\(\Rightarrow y_{min}=-41\) ; \(y_{max}=40\)
b. Trên [0;5] ta có:
\(y\left(0\right)=35\) ; \(y\left(3\right)=8\); \(y\left(5\right)=40\)
\(\Rightarrow y_{max}=40\) ; \(y_{min}=8\)

Giá trị nhỏ nhất của hàm số trên đoạn [-2,3] là điểm thấp nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị nhỏ nhất tại x = -2. Thay x = -2 vào hàm số y đã cho ta có giá trị nhỏ nhất là -2.
Giá trị lớn nhất của hàm số trên đoạn [-2,3] là điểm cao nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị lớn nhất tại x = 3. Thay x = 3 vào hàm số y đã cho ta có giá trị lớn nhất là 3.

\(y'=\dfrac{3}{\left(x+2\right)^2}>0\Rightarrow\) hàm đồng biến trên đoạn đã cho
\(\Rightarrow\max\limits_{\left[0;1\right]}y=y\left(1\right)=0\)
Đáp án là C