Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
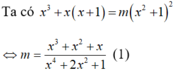
Xét hàm số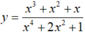 
xác định trên R.
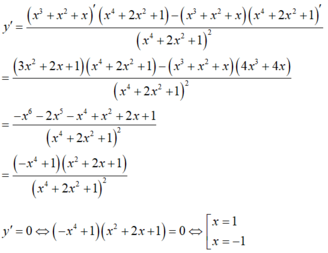
Bảng biến thiên
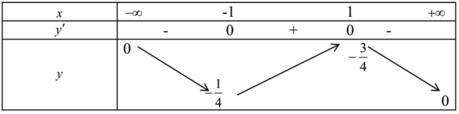
Phương trình (1) có nghiệm thực khi đường thẳng y= m cắt đồ thị hàm số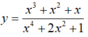 
Khi và chỉ khi -1/4 ≤ m≤ 3/4
Chọn D.
a, Với m=1 thay vào pt
Ta có
\(x^2+x-1=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{-1+\sqrt{5}}{2}\\x=\dfrac{-1-\sqrt{5}}{2}\end{matrix}\right.\)
b,
Thay x=2 vào pt
ta có
\(4-2-3m+2=0\)
\(\Leftrightarrow4-3m=0\)
\(\Rightarrow m=\dfrac{4}{3}\)
c, Ta có
\(\Delta=1-4\left(-3m+2\right)\)
\(=12m-7\)
Để pt có 2 nghiệm phân biệt thì \(\Delta>0\)
\(\Rightarrow12m-7>0\)
\(\Rightarrow m>\dfrac{7}{12}\)
d,
Để ptcos nghiệm kép thì \(\Delta=0\)
\(\Rightarrow12m-7=0\)
\(\Rightarrow m=\dfrac{7}{12}\)
e,
Để pt vô nghiệm thì \(\Delta< 0\)
\(\Rightarrow m< \dfrac{7}{12}\)
Chọn C
Bất phương trình x - 1 x + 1 ≥ m có nghiệm thuộc [1;2]
⇒ hàm số y = f x là hàm đồng biến
⇒ m ≤ 1 3
Chọn C
Bất phương trình x - 1 x + 1 ≥ m có nghiệm thuộc [1;2]
Xét hàm số f x = x - 1 x + 1 trên [1;2] ta có
⇒ hàm số y = f x là hàm đồng biến.
⇒ m ≤ 1 3
Đáp án C
Mà phương trình f t = m ⇒ để phương trình có nghiệm thì m ∈ 2 2 ; 3 .