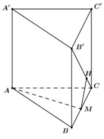
Cho hình lăng trụ đều ABC.A’B’C’. Gọi M, M’, I lần lượt là trung điểm của BC, B’C’ và AM. Khoảng cách giữa đường thẳng BB’ và mp(AMM’A’) bằng độ dài đoạn thẳng:
A. BM’
B. BI
C. BM
D. BA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 11 2017
Đáp án B
Phương pháp : Dụng đường vuông góc chung.
Cách giải :
Ta có: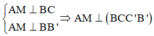 
Trong (BCC’B’) kẻ 
=>MH là đoạn vuông góc chung giữa AM và B’C 
Dễ thấy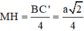 
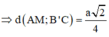
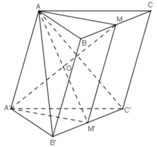
CM
20 tháng 3 2018
a) Do ABC.A’B’C’ là hình lăng trụ nên ta có: BCC’B’ là hình bình hành
Xét tứ giác BCC’B’ có M và M’ lần lượt là trung điểm của BC và B’C’ nên MM’ là đường trung bình
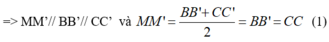
Lại có: AA’// BB’ và AA’= BB’ ( tính chất hình lăng trụ) (2)
Từ (1) và (2) suy ra: MM’// AA’ và MM’ = AA’
=> Tứ giác AMM’A’ là hình bình hành
b) Trong (AMM’A’) gọi O = A’M ∩ AM’, ta có :
Ta có : O ∈ AM’ ⊂ (AB’C’)
⇒ O = A’M ∩ (AB’C’).
c)
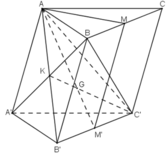
Gọi K = AB’ ∩ BA’, ta có :
K ∈ AB’ ⊂ (AB’C’)
K ∈ BA’ ⊂ (BA’C’)
⇒ K ∈ (AB’C’) ∩ (BA’C’)
Dễ dàng nhận thấy C’ ∈ (AB’C’) ∩ (BA’C’)
⇒ (AB’C’) ∩ (BA’C’) = KC’.
Vậy d cần tìm là đường thẳng KC’
d) Trong mp(AB’C’), gọi C’K ∩ AM’ = G.
Ta có: G ∈ AM’ ⊂ (AM’M)
G ∈ C’K.
⇒ G = (AM’M) ∩ C’K.
+ K = AB’ ∩ A’B là hai đường chéo của hình bình hành ABB’A’
⇒ K là trung điểm AB’.
ΔAB’C’ có G là giao điểm của 2 trung tuyến AM’ và C’K
⇒ G là trọng tâm ΔAB’C’.
Đáp án C
Vì ABC.A’B’C’ là lăng trụ đều nên B C ⊥ B B ’ , tam giác ABC là tam giác đều ⇒ A M ⊥ B C .
Mặt khác vì M và M’ là trung điểm của BC và B’C’ nên MM’BB’, suy ra B C ⊥ M M ’ . Từ đó ta được B C ⊥ ( A M M ’ A ’ ) và B B ’ | | A M M ’ A ’ . Vậy khoảng cách giữa đường thẳng BB’ và mp(AMM’A’) bằng khoảng cách từ điểm B đến mặt phẳng (AMM’A’), hay là bằng độ dài đoạn thẳng BM