Cho khối lăng trụ đều A B C . A ' B ' C ' có A B = a 3 , góc giữa đường thẳng A ' B và mặt phẳng (ABC) bằng 45 0 . Thể tích khối lăng trụ đã cho bằng
A. 3 2 a 3 8
B. 3 a 3 4
C. 9 2 a 3 8
D. 9 a 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Góc giữa B′C và mặt đáy (ABC) bằng 300 nên
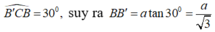
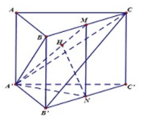
Gọi M,N lần lượt là trung điểm của BC,B′C′.
![]()
mà (A′BC) chứa A′C nên:
![]()
Kẻ NHvuông góc với AM, ta có
![]()
![]()
![]()
![]()
Ta có

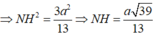
Vậy
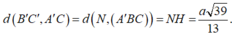

Gọi H là trung điểm của AB, \(A'H\perp\left(ABC\right)\) và \(\widehat{A'CH}=60^0\)
Do đó \(A'H=CH.\tan\widehat{A'CH}=\frac{3a}{2}\)
Do đó thể tích khối lăng trụ là \(V_{ABC.A'B'C'}=\frac{3\sqrt{3}a^3}{8}\)
Gọi I là hình chiếu vuông góc của H lên AC; K là hình chiếu vuông góc của H lên A'I. Suy ra :
\(HK=d\left(H,\left(ACC'A'\right)\right)\)
Ta có :
\(HI=AH.\sin\widehat{IAH}=\frac{\sqrt{3}a}{4}\);
\(\frac{1}{HK^2}=\frac{1}{HI^2}+\frac{1}{HA'^2}=\frac{52}{9a^2}\)
=>\(HK=\frac{3\sqrt{13}a}{26}\)
Do đó \(d\left(B;\left(ACC'A'\right)\right)=2d\left(H;\left(ACC'A'\right)\right)=2HK=\frac{3\sqrt{13}a}{13}\)

Đáp án A
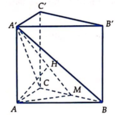
Gọi M là trung điểm của BC thì B C ⊥ A ' A M .
Từ A kẻ A H ⊥ A ' M , H ∈ A ' M . Khi đó A H ⊥ ( A ' B C ) .
Suy ra d A , A ' B C = A H = a 5 2 .
Góc giữa đường thẳng A ' B và mặt phẳng (ABC) bằng góc A ' M A ⏞ .
Theo giả thiết ta có A ' M A ⏞ = 60 °
Đặt AB = 2x thì A M = x 3 ; A ' A = 2 x 3 .
Suy ra A H = A ' A . A M A ' A 2 + A M 2 = 2 x 15 5
Từ giả thiết ta có 2 x 15 5 = a 5 2 ⇒ x = 5 a 15 12 Do đó
A A ' = 5 a 2 ; S A B C = 25 a 2 3 48
Vậy thể tích khối lăng trụ ABC.A'B'C' là V = 125 3 96 a 3 .