Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, A B = 6 a , A C = 5 a , A D = 4 a . Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
A. V = 5 a 3 3 .
B. V = 20 a 3 3 .
C. V = 5 a 3
D. V = 10 a 3

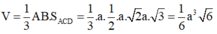

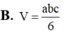
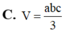
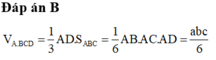
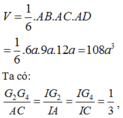
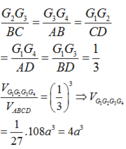



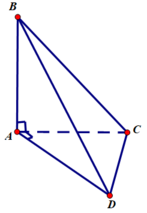
Chọn C.
Phương pháp:
+) Thể tích khối tứ diện OABC có OA, OB, OC đôi một vuông góc và có độ dài các cạnh đó lần lượt là a, b, c là: V = 1 6 a b c
Cách giải: