Xét khối tứ diện ABCD,AB= x, các cạnh còn lại bằng 2 3 . Tìm x để thể tích khối tứ diện ABCD lớn nhất
A. x = 6
B. x = 2 2
C. x = 14
D. x = 3 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
6 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
CM
13 tháng 1 2018
Đáp án B
Đặt a=2. Gọi H là trung điểm của BC khi đó A H ⊥ B C D H ⊥ B C
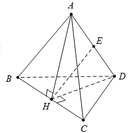
Suy ra B C ⊥ A H D và ta có A H = D H = a 3 2
Gọi E là trung điểm của AD do tam giác AHD cân nên
H E ⊥ A D ⇒ H E = A H 2 − A E 2 = 3 a 2 4 − x 2 4
Ta có V A B C D = V B . A H D + V C . A H D
= 1 3 B C . S A H D = 1 3 a . 1 2 H E . A D
Lại có:
3 a 2 4 − x 2 4 . x = 2 3 a 2 4 − x 2 4 . x 2 ≤ 3 a 2 4 − x 2 4 + x 2 4
= 3 a 2 4 ⇒ V A B C D ≤ a 3 8 ⇒ V max = a 3 8 .
Dấu bằng xảy ra 3 a 2 = 2 x 2 ⇔ x = a 6 2 = 6
Cách 2: Nhận xét V max ⇔ S A H D lớn nhất 1 2 A H . D H sin A H D ⏜ = 3 a 2 8 . sin A H D ⏜ ≤ 3 a 2 8
CM
18 tháng 4 2019
Đáp án C
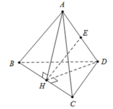
Gọi H là trung điểm BC khi đó A H ⊥ B C D H ⊥ B C
SUY RA B C ⊥ A H D và ta có A H = D H = a 3 2
Gọi E là trung điểm của AD do tam giác AHD cân nên
H E ⊥ A D ⇒ H E = A H 2 − A E 2 = 3 a 2 4 − x 2 4
Ta có V A B C D = V B A H D + V C A H D = 1 3 B C . S A H D = 1 3 a 1 2 H E . A D
Lại có
3 a 2 4 − x 2 4 . x = 2. 3 a 2 4 − x 2 4 . x 2 ≤ 3 a 2 4 − x 2 4 + x 2 4 = 3 a 2 4 ⇒ V A B C D ≤ a 3 8 ⇒ V m a x = a 3 8
Dấu bằng xảy ra khi và chỉ khi 3 a 2 = 2 x 2 ⇔ x = a 6 2 = 3 2
