Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
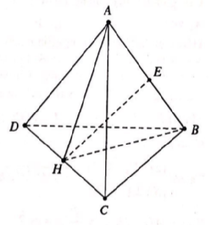
Đặt a=2. Gọi H là trung điểm của BC khi đó A H ⊥ B C D H ⊥ B C
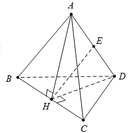
Suy ra B C ⊥ A H D và ta có A H = D H = a 3 2
Gọi E là trung điểm của AD do tam giác AHD cân nên
H E ⊥ A D ⇒ H E = A H 2 − A E 2 = 3 a 2 4 − x 2 4
Ta có V A B C D = V B . A H D + V C . A H D
= 1 3 B C . S A H D = 1 3 a . 1 2 H E . A D
Lại có:
3 a 2 4 − x 2 4 . x = 2 3 a 2 4 − x 2 4 . x 2 ≤ 3 a 2 4 − x 2 4 + x 2 4
= 3 a 2 4 ⇒ V A B C D ≤ a 3 8 ⇒ V max = a 3 8 .
Dấu bằng xảy ra 3 a 2 = 2 x 2 ⇔ x = a 6 2 = 6
Cách 2: Nhận xét V max ⇔ S A H D lớn nhất 1 2 A H . D H sin A H D ⏜ = 3 a 2 8 . sin A H D ⏜ ≤ 3 a 2 8

Đáp án C
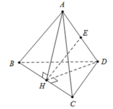
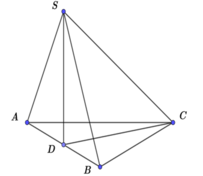
Gọi H là trung điểm BC khi đó A H ⊥ B C D H ⊥ B C
SUY RA B C ⊥ A H D và ta có A H = D H = a 3 2
Gọi E là trung điểm của AD do tam giác AHD cân nên
H E ⊥ A D ⇒ H E = A H 2 − A E 2 = 3 a 2 4 − x 2 4
Ta có V A B C D = V B A H D + V C A H D = 1 3 B C . S A H D = 1 3 a 1 2 H E . A D
Lại có
3 a 2 4 − x 2 4 . x = 2. 3 a 2 4 − x 2 4 . x 2 ≤ 3 a 2 4 − x 2 4 + x 2 4 = 3 a 2 4 ⇒ V A B C D ≤ a 3 8 ⇒ V m a x = a 3 8
Dấu bằng xảy ra khi và chỉ khi 3 a 2 = 2 x 2 ⇔ x = a 6 2 = 3 2

Đáp án B
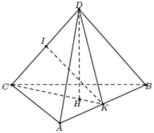
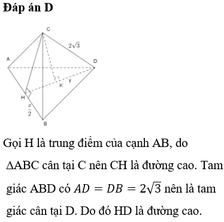
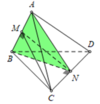
Gọi K là trung điểm của AB, do ∆CAB và ∆DAB là hai tam giác cân chung cạnh đáy AB nên C K ⊥ A B D K ⊥ A B ⇒ A B ⊥ C D K
Kẻ D H ⊥ C K ta có D H ⊥ A B C
Vậy V = 1 3 S . h = 1 3 1 2 C K . A B . D H = 1 3 1 2 C K . D H . A B
Suy ra V = 1 3 A B . S Δ K D C
Dễ thấy Δ C A B = Δ D A B ⇒ C K = D K h a y Δ K D C cân tại K. Gọi I là trung điểm CD, suy ra K I ⊥ C D và K I = K C 2 − C I 2 = A C 2 − A K 2 − C I 2 = 4 − x 2 4 − 1 = 1 2 12 − x 2
Suy ra S Δ K D C = 1 2 K I . C D = 1 2 12 − x 2
Vậy V = 1 6 x 12 − x 2 ≤ 1 6 . x 2 + 12 − x 2 2 = 1 . Dấu đẳng thức xảy ra khi và chỉ khi x = 12 − x 2 h a y x = 6








Chọn A.