Tìm tất cả các giá trị thực của m để hàm số y = m ln x − 2 ln x = m − 1 nghịch biến trên e 2 ; + ∞ .
A. m ≤ − 2 hoặc m = 1
B. m < − 2 hoặc m = 1
C. m < − 2
D. m < − 2 hoặc m > 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: y ' = 2 x x 2 + 1 = - m .
Hàm số Y= ln( x2+ 1) –mx+1 đồng biến trên R khi và chỉ khi y’≥ 0 với mọi x.
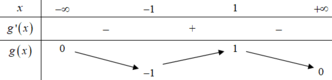
⇔ g ( x ) = 2 x x 2 + 1 ≥ m , ∀ x ∈ - ∞ ; + ∞ . g ' ( x ) = - 2 x 2 + 2 ( x 2 + 1 ) 2 = 0 ⇔ x = ± 1 .
Bảng biến thiên:
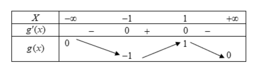
Dựa vào bảng biến thiên ta có: g ( x ) = 2 x x 2 + 1 ≥ m với mọi x khivà chỉ khi m≤ -1.
Chọn C.

Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
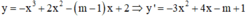
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
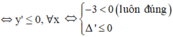
![]()
![]()
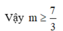

Chọn đáp án C
Phương pháp
Hàm số y=f(x) có TXĐ D=R đồng biến trên nếu:

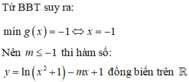

Chọn B.
Tập xác định ![]()
Có 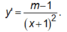
Hàm số nghịch bến trên mỗi khoảng của tập xác định
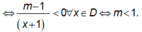
Đáp án C
Đặt t = ln x , vì x ∈ e 2 ; + ∞ ⇒ t ∈ ( 2 ; + ∞ )
Tìm m để hàm số y = m t − 2 t − m − 1 nghịch biến trên ( 2 ; + ∞ )
Ta có y ' = − m 2 − m + 2
Theo trên có y ' < 0 m + 1 ≤ 2 ⇒ − m 2 − m + 2 < 0 m ≤ 1 ⇔ m < − 2