Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
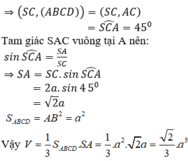
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
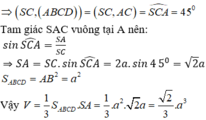
Đáp án A.
Phương pháp
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đáy.
Cách giải
S C ; A B C D = S C ; A C = S C A
ABCD là hình vuông cạnh a ⇒ A C = a 2
Xét tam giác vuông SAC có:
tan = S A A C = 2 a a 2 = 2
Đáp án A
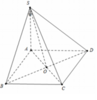
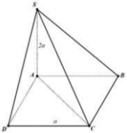
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .
Đáp án C
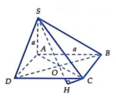
Gọi H là hình chiếu của C trên SO(O = AC ∩ BD), vì góc SOC tù nên H nằm ngoài SO
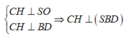
=> Góc tạo bởi SC và (SBD) là C S O ^
Ta có 
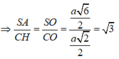
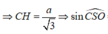
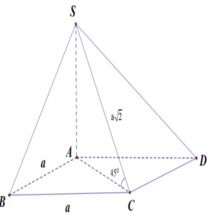
Do \(\left(SC;\left(ABCD\right)\right)=45^0;SA\perp\left(ABCD\right)\)
nên \(\left\{{}\begin{matrix}\left(SC;AC\right)=45^0\\AS\perp AC\end{matrix}\right.\)\(\Rightarrow AS=AC=\sqrt{AB^2+BC^2}=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{6}.\left(AD+BC\right).AB.AS\)
\(=\dfrac{1}{6}\left(2a+a\right).a.a\sqrt{2}=\dfrac{\sqrt{2}}{2}a^3\)
Đáp án B
Phương pháp giải:
Dựng hình, xác định góc và sử dụng hệ thức lượng trong tam giác để tính tang
Lời giải:
Vì SA ⊥ (ABCD) => AC là hình chiếu của SC trên (ABCD)
Suy ra SC; (ABCD) = (SC; AC) = SCA = α(00; 900)
Tam giác SAC vuông tại A, có
Vậy tan góc giữa đường thẳng SC và mặt phẳng (ABCD) là 1 2