Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m 3 x 3 + 7 m x 2 + 14 x - m + 2 nghịch biến trên nửa khoảng [ 1 ; + ∞ ) ?
A. - ∞ ; - 14 15
B. ( - ∞ ; - 14 15 ]
C. - 2 ; - 14 15
D. [ - 14 15 ; + ∞ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C
Tập xác định : D = R \{m}
Ta có : y ' = 1 − m x − m 2
Hàm số nghịch biến trên khoảng (−¥;2) khi và chỉ khi y' <0, "x < 2, tức là : 1 − m < 0 m ≥ 2 ⇔ m ≥ 2 . Vậy tập giá trị m cần tìm là [2; + ∞ )

Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
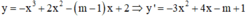
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
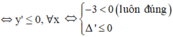
![]()
![]()
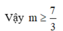

Chọn A.
Tập xác định:D= R. Ta có:y ‘= m-3 + (2m+1).sinx
Hàm số nghịch biến trên R
![]()
Trường hợp 1: m= -1/ 2 ; ta có 0 ≤ 7 2 ∀ x ∈ ℝ
Vậy hàm số luôn nghịch biến trên R.
Trường hợp 2: m< -1/ 2 ; ta có
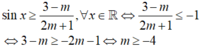
Trường hợp 3:m > -1/2 ; ta có:
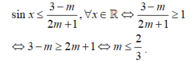
Vậy - 4 ≤ m ≤ 2 3

y'= \(4x^3-4\left(m-1\right)x\)
Để hàm số đồng biến trên khoảng (1;3) thì \(y'\left(x\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow x^2-\left(m-1\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow m-1\le x^2,\forall x\in\left(1;3\right)\)
\(\Rightarrow m-1\le1\Leftrightarrow m\le2\)
Vậy \(m\in\) (−\(\infty\);2]
Đáp án B