Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình log 2 ( x 2 - 3 x + 2 m ) = log 2 ( x + m ) có nghiệm thực
A. Mười.
B. Chín.
C. Vô số.
D. Tám
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Điều kiện 40 < x < 60
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.

ĐKXĐ: \(-x^2+4x+m>0\)
\(log_2\left(-x^2+4x+m\right)-log_2\left(x^2+2\right)< log_23\)
\(\Leftrightarrow log_2\left(\dfrac{-x^2+4x+m}{x^2+2}\right)< log_23\)
\(\Leftrightarrow\dfrac{-x^2+4x+m}{x^2+2}< 3\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x^2+4x+m>0\\-x^2+4x+m< 3x^2+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>x^2-4x\\m< 4x^2-4x+6\end{matrix}\right.\) ; \(\forall x\in\left[1;5\right]\)
Xét hai hàm \(\left\{{}\begin{matrix}f\left(x\right)=x^2-4x\\g\left(x\right)=4x^2-4x+6\end{matrix}\right.\) trên \(\left[1;5\right]\) ta được: \(\left\{{}\begin{matrix}f\left(x\right)_{max}=f\left(5\right)=5\\g\left(x\right)_{min}=g\left(1\right)=6\end{matrix}\right.\)
\(\Rightarrow5\le m\le6\)
Có 2 giá trị nguyên của m

ĐKXĐ: \(x\ge0\)
\(x^2+1+\left(2-m\right)x-2\sqrt{x\left(x^2+1\right)}=0\)
Với \(x=0\) ko phải nghiệm, với \(x>0\) chia 2 vế cho x:
\(\Rightarrow\dfrac{x^2+1}{x}+2-m-2\sqrt{\dfrac{x^2+1}{x}}=0\)
Đặt \(\sqrt{\dfrac{x^2+1}{x}}=t\ge\sqrt{2}\)
\(\Rightarrow t^2-2t+2=m\)
Xét hàm \(f\left(t\right)=t^2-2t+m\) khi \(t\ge\sqrt{2}\)
\(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=1< \sqrt{2}\end{matrix}\right.\) \(\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge\sqrt{2}\)
\(\Rightarrow f\left(t\right)\ge f\left(\sqrt{2}\right)=4-2\sqrt{2}\)
\(\Rightarrow\) Pt có nghiệm khi \(m\ge4-2\sqrt{2}\)

Chọn đáp án A
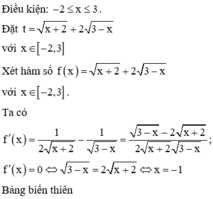
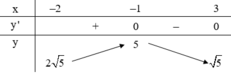

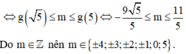
Vậy số giá trị nguyên của m để phương trình có nghiệm là 10.