Cho phương trình 2 x = m .2 x . c o s π x − 4 , với m là tham số thực. Gọi m 0 là giá trị của m sao cho phương trình trên có đúng một nghiệm thực. Khẳng định nào dưới đây đúng?
A. m 0 ∈ − 5 ; − 1
B. m 0 < − 5
C. m 0 ∈ − 1 ; 0
D. m 0 > 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Đặt t = sin x , t ∈ − 1 ; 1 . Phương trình đã cho trở thành 2 t + 1 t + 2 = m (*).
Để phương trình đã cho có đúng hai nghiệm thuộc đoạn 0 ; π thì phương trình (*) phải có đúng một nghiệm thuộc nửa khoảng 0 ; 1 .
Xét hàm số f t = 2 t + 1 t + 2 . Ta có f ' t = 3 t + 2 2 .
Bảng biến thiên của :
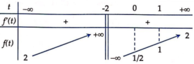
Vậy để phương trình (*) có đúng một nghiệm thuộc nửa khoảng 0 ; 1 thì m ∈ 1 2 ; 1 . Vậy C là đáp án đúng

Đáp án B.
Với x ∈ 5 2 ; 4 thì phương trình tương đương với:
m - 1 log 2 2 x - 2 + m - 5 log 2 x - 2 + m - 1 = 0 (1)
Đặt log 2 ( x - 2 ) = t . Với x ∈ 5 2 ; 4 thì t ∈ - 1 ; 1 . Phương trình (1) trở thành:
( m - 1 ) t 2 + ( m - 5 ) t + m - 1 = 0 ⇔ m ( t 2 + t + 1 ) = t 2 + 5 t + 1 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 (2)
Xét hàm số f ( t ) = t 2 + 5 t + 1 t 2 + t + 1 = 1 + 4 t t 2 + t + 1 trên đoạn - 1 ; 1 .
Đạo hàm f ' ( t ) = - 4 ( t 2 - 1 ) t 2 + t + 1 ≥ 0 , ∀ t ∈ - 1 ; 1 ; f ' ( t ) = 0 ⇔ t = ± 1 . Khi đó hàm số f ( t ) đồng biến trên - 1 ; 1 . Suy ra min - 1 ; 1 f ( t ) = f ( - 1 ) = - 3 ; max - 1 ; 1 f ( t ) = f ( 1 ) = 7 3 .
Phương trình (2) có nghiệm ⇔ Đường thẳng y - m cắt đồ thị hàm số f ( t ) ⇔ - 3 ≤ m ≤ 7 3 . Vậy S = - 3 ; 7 3 → a = - 3 , b = 7 3 → a + b = - 3 + 7 3 = - 2 3 .

Lời giải:
Đặt $\sqrt{x+2}=t(t\geq 0)$ thì pt trở thành:
$t^2-2-2t-m-3=0$
$\Leftrightarrow t^2-2t-(m+5)=0(*)$
Để PT ban đầu có 2 nghiệm pb thì PT $(*)$ có 2 nghiệm không âm phân biệt.
Điều này xảy ra khi \(\left\{\begin{matrix} \Delta'=1+m+5>0\\ S=2>0\\ P=-(m+5)\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-6\\ m\leq -5\end{matrix}\right.\)
Đáp án B.

\(x^2-2\left(m-3\right)x-6m-7\\\Delta'=\left(m-3\right)^2-\left(-6m-7\right)=m^2-6m+9+6m+7\\ =m^2+16>0\forall m\)
=> pt luôn có 2 no pb
theo viet \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2\left(m-3\right)\\x_1.x_2=-6m-7\end{matrix}\right.\)
\(C=\left(x_1+x_2\right)^2+8x_1x_2\\ =\left[2\left(m-3\right)\right]^2+8\left(-6m-7\right)\\ =4\left(m-3\right)^2-48m-56\\ =4\left(m^2-6m+9\right)-48m-56\\ =4m^2-72m-20\\ =\left(2m\right)^2-2.2m.18+18^2-344\\ =\left(2m-18\right)^2-344\)
có \(\left(2m-18\right)^2\ge0\forall m\\ \Rightarrow\left(2m-18\right)^2-344\ge-344\)
vậy..
\(C=\left(x_1+x_2\right)^2+8x_1x_2\)
\(=\left(2m-6\right)^2+8\left(-6m-7\right)\)
\(=4m^2-24m+36-48m-56\)
\(=4m^2-72m-20\)
\(=4m^2-72m+324-344\)
\(=\left(2m-18\right)^2-344\ge-344\forall x\)
Dấu '=' xảy ra khi m=9

a)Ta có: \(\Delta\)= m2 - 4(m - 1) = m2 - 4m + 4 = (m - 2)2 \(\geq\)0 với mọi m
Vậy: PT có 2 nghiệm x1, x2 với mọi m
b)Theo Vi-et: x1 + x2 = m và x1x2 = m - 1
Do đó: A = x12 + x22 - 6x1x2 = (x1 + x2)2 - 8x1x2 = m2 - 8(m - 1) = m2 - 8m + 8 = ( m2 - 8m + 16) - 8 = (m - 4)2 - 8 \(\geq\)- 8 với mọi m
đúng nhé
Vậy: GTNN của A là -8 <=> m = 4
Phương pháp:
- Biến đổi phương trình và nhận xét tính đối xứng của nghiệm.
- Tìm điều kiện để phương trình có nghiệm duy nhất suy ra m.
Cách giải:
Do đó để phương trình có đúng một nghiệm thực thì