Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ
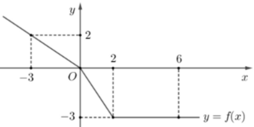
Tích phân ∫ - 3 6 f ( x ) d x bằng
A. 12
B. -15
C. -12
D. 15
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 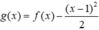 có
có
![]()
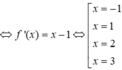
Vì đường thẳng y=x-1 cắt đồ thị f '(x) tại 4 điểm có hoành độ x=-1, x=1, x=2, x=3
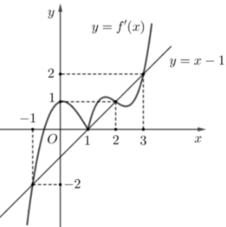

Suy ra g(x) có ba điểm cực trị là x=-1, x=1, x=2, x=3
Theo giả thiết  có nên g(x)=0 có hai nghiệm phân biệt (là nghiệm đơn hoặc bội lẻ). Vậy hàm số y=|g(x)| có tổng cộng 3 + 2 = 5 điểm cực trị.
có nên g(x)=0 có hai nghiệm phân biệt (là nghiệm đơn hoặc bội lẻ). Vậy hàm số y=|g(x)| có tổng cộng 3 + 2 = 5 điểm cực trị.
Chọn đáp án B.
*Chú ý số điểm cực trị của hàm số y=|g(x)| bằng tổng số điểm cực trị của f(x) và số nghiệm đơn (hoặc bội lẻ) của phương trình f(x)=0
Chọn đáp án B.

Đổi biến ![]()
![]()
Do đó
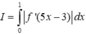
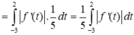

Trên đoạn [-3;-1] đồ thị f(t) đi xuống nên ![]() trên đoạn [-1;2] đồ thị f(t) đi lên nên
trên đoạn [-1;2] đồ thị f(t) đi lên nên ![]()
Vì vậy
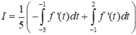
![]()
![]()
Chọn đáp án B.

Chọn đáp án D
![]()
![]()
![]()
![]()
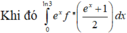
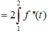

![]()
Do hàm số đạt cực đại tại điểm x=1⇒ f′(1) = 0 và đường thẳng Δ qua hai điểm (0;−3);(1;0) nên có phương trình y=3x−3.
Vì Δ là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 ⇒ f ' ( 2 ) = k △ =3
Vậy
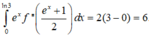
Áp dụng diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) và trục hoành có:
Chọn đáp án C.