Cho hình lập phương ABCD. A ' B ' C ' D ; cạnh bằng a. Gọi O là giao điểm của AC và BD. Thể tích của tứ diện O A ' B C bằng
A. a 3 12
B. a 3 24
C. a 3 6
D. a 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi M, N lần lượt là trung điểm các cạnh A′B′,C′D′ ta có ((OA′B′), (OC′D′)) = (OM,ON).
Ta có
MN=a, 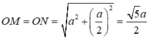
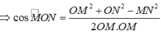
= 3 5
Chọn đáp án D.

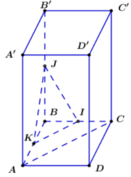
Gọi K là trung điểm của AB ⇒ IK // BC (tính chất đường trung bình của tam giác)
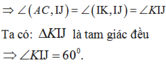
Chọn B.

THAM KHẢO:

a) Vì AA′⊥(ABCD) nên góc giữa đường thẳng AA' và (ABCD) là \(90^0\)
b) CC′⊥(ABCD) nên C là hình chiếu vuông góc của C' lên (ABCD).
Suy ra góc giữa BC' và (ABCD) là \(\widehat{C'BC}\)=\(45^O\) (Vì BCC'C' là hình vuông)c) Gọi cạnh của hình lập phương là a
Ta có: AC=\(a\sqrt{2}\),tan \(\widehat{ACA'}\)=\(\dfrac{1}{\sqrt{2}}\) nên \(\widehat{ACA'}\)=\(35^O\)
AA′⊥(ABCD) nên A là hình chiếu vuông góc của A' lên (ABCD)
Suy ra góc giữa A'C và (ABCD) là \(\widehat{ACA'}\)=\(35^O\)