Trong không gian Oxyz cho A(-3;2;4) và B(5;2;2). Mặt phẳng (P) x+y-3z+4= 0. Biết đường thẳng AB cắt mp(P) tại điểm M. Tính tỉ số MA/MB bằng
A. 1. B. 9/5. C. 5/9. D. căn 68 /11 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 2 2018
Ta có điểm tiếp xúc là h/c(A,(Oxyz))=N(0;-1;1)
Chọn đáp án B.
CM
7 tháng 8 2018
Chọn B
Gọi M (x; y; z)
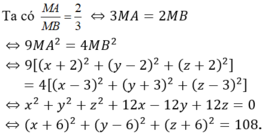
Như vậy, điểm M thuộc mặt cầu (S) tâm I(-6;6;-6) và bán kính R = √108 = 6√3. Do đó OM lớn nhất bằng
CM
3 tháng 12 2019
Đáp án B
Phương pháp:
Hai vectơ
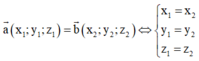
Cách giải:
Gọi điểm B x 0 ; y 0 ; z 0 là điểm cần tìm. Khi đó
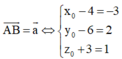
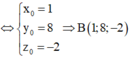
\(\overrightarrow{AB}=\left(8;0;-2\right)=2\left(4;0;-1\right)\)
Phương trình AB có dạng: \(\left\{{}\begin{matrix}x=5+4t\\y=2\\z=2-t\end{matrix}\right.\)
Tọa độ M thỏa mãn:
\(5+4t+2-3\left(2-t\right)+4=0\) \(\Rightarrow t=-\dfrac{5}{7}\)
\(\Rightarrow M\left(\dfrac{15}{7};2;\dfrac{19}{7}\right)\) \(\Rightarrow\left\{{}\begin{matrix}MA=\dfrac{9\sqrt{17}}{7}\\MB=\dfrac{5\sqrt{17}}{7}\end{matrix}\right.\)
\(\Rightarrow\dfrac{MA}{MB}=\dfrac{9}{5}\)