Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 a , S A = S B = a 2 khoảng cách từ A đến mặt phẳng (SCD) bằng a. Thể tích của khối chóp đã cho bằng
A. 2 a 3 3 3
B. a 3 6 3
C. a 3 3 6
D. 2 a 3 6 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là trung điểm của AB, suy ra \(SH\perp\left(ACBD\right)\)
Do đó \(SH\perp HD\) ta có :
\(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
Suy ra \(V_{s.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{a^2}{3}\)
Gọi K là hình chiếu vuông góc của H trên BD và E là hình chiếu vuông góc của H lên SK. Ta có :
\(\begin{cases}BD\perp HK\\BD\perp SH\end{cases}\) \(\Rightarrow BH\perp\) (SHK)
=> \(BD\perp HE\) mà \(HE\perp SK\) \(\Rightarrow HE\perp\) (SBD)
Ta có : HK=HB.\(\sin\widehat{KBH}\)\(=\frac{a\sqrt{2}}{4}\)
Suy ra \(HE=\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{a}{3}\)
Do đó \(d\left(A:\left(SBD\right)\right)\)=2d(H; (SBD)) =3HE=\(\frac{2a}{3}\)

1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.
2) Ta có tam giác SAB đều nên SA =a3√2
suy ra V=13SABCD.SH=a33√6

Đáp án là D
Đặt A B = x ta có S C 2 = S A 2 + 2 x 2 = 3 a 2 S B 2 = S A 2 + x 2 = 2 a 2 ⇔ S A = x = a ⇒ d A ; ( S C D ) = a 2
Gọi H=h/c(S,(ABCD)) ta có ∆ S H A = ∆ S H B ( c - g - c ) ⇒ H A = H B vì vậy H nằm trên đường trung trực của đoạn thẳng AB đồng thời cũng là đường trung trực của CD.
Gọi M,N lần lượt là trung điểm các cạnh AB,CD. Hạ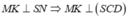
Tam giác SMN có MN=2a,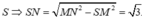 và đường cao hạ từ đỉnh M là
và đường cao hạ từ đỉnh M là
MK=d(M,(SCD))=d(A,(SCD))=a. Do đó M K = S M = a ⇒ K ≡ S . Vì vậy ∆ S M N vuông tại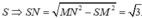 a.
a.
Vì vậy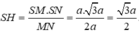
Do đó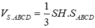
Chọn đáp án A.