Cho tam giác ABC đều, trên nửa mặt phẳng BC không chứa A, vẽ nửa đường tròn đường kính BC. Lấy DE trên nửa đường tròn sao cho cung BD = cung DE = cung EC. Gọi I, J lần lượt là giao điểm AD, AE với BC. CMR BI = IJ = JC.
Tớ vẽ hình rồi :((( Tớ cần giúp gấp. Mọi người giúp tớ với...mai tớ phải nộp rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 3 2021
a) Gọi O là trung điểm của BC.
Ta có \(\stackrel\frown{BD}=\stackrel\frown{DE}=\stackrel\frown{EC}\Rightarrow\widehat{BOD}=\widehat{DOE}=\widehat{EOC}=60^o\).
Từ đó CE // AB, BD // AC.
Suy ra \(\Delta ABN\sim\Delta ECN\).
b) Theo tính đối xứng ta có BM = CN.
Ta có \(\dfrac{BN}{NC}=\dfrac{AB}{CE}=\dfrac{AB}{CO}=2\Rightarrow BN=2NC\Rightarrow MN=NC\).
Dễ dàng suy ra đpcm.
1 tháng 2 2022
a) Tứ giác ACDE là hình vuông (gt).
\(\Rightarrow\) \(\widehat{DAE}=\widehat{DAC}\) (Tính chất hình vuông).
Xét tứ giác AMCB:
\(A;M;C;B\in\left(O\right)\left(gt\right).\)
\(\Rightarrow\) Tứ giác AMCB nội tiếp (O).
\(\Rightarrow\) \(\left\{{}\begin{matrix}\widehat{MCB}=\widehat{DAE}.\\\widehat{MBC}=\widehat{DAC}.\end{matrix}\right.\)
Mà \(\widehat{DAE}=\widehat{DAC}\left(cmt\right).\)
\(\Rightarrow\widehat{DAE}=\widehat{DAC}=\widehat{MCB}=\widehat{MBC}.\)
Xét (O):
\(M\in\left(O\right)\left(gt\right).\)
BC là đường kính (gt).
\(\Rightarrow\widehat{BMC}=90^o\) (Góc nội tiếp chắn nửa đường tròn).
Xét \(\Delta BMC:\)
\(\widehat{MCB}=\widehat{MBC}\left(cmt\right).\)
\(\Rightarrow\text{}\Delta BMC\) cân tại M.
Mà \(\widehat{BMC}=90^o\left(cmt\right).\)
\(\Rightarrow\text{}\Delta BMC\) vuông cân tại M.
b) Tứ giác ACDE là hình vuông (gt).
\(\Rightarrow\) \(\widehat{AED}=\widehat{EDC}=\widehat{DCA}=\widehat{CAE}=90^o\) (Tính chất hình vuông).
Xét tứ giác FDCM:
\(\widehat{FMC}+\widehat{FDC}=90^o+90^o=180^o.\)
Mà 2 góc ở vị trí đối nhau.
\(\Rightarrow\) Tứ giác FDCM nội tiếp đường tròn.
\(\Rightarrow\widehat{FCM}=\widehat{FDM}.\)
Mà \(\widehat{FDM}+\widehat{EAD}=90^o\) (2 góc phụ nhau).
\(\Rightarrow\widehat{FCM}+\widehat{EAD}=90^o.\)
Lại có \(\widehat{EAD}=\widehat{MCB}\left(cmt\right).\)
\(\Rightarrow\widehat{FCM}+\widehat{MCB}=90^o.\\ \Rightarrow\widehat{FCB}=90^o.\)
Xét tứ giác BEFC:
\(\widehat{FCB}+\widehat{FEB}=90^o+90^o=180^o.\)
Mà 2 góc ở vị trí đối nhau.
\(\Rightarrow\) Tứ giác BEFC nội tiếp đường tròn.
c) Xét (O):
BC là đường kính (gt).
\(FC\perp BC\left(\widehat{FCB}=90^o\right).\)
\(\Rightarrow\) FC là là tiếp tuyền của đường tròn (O).
2 tháng 3 2023
a: góc ADB=1/2*sđ cung AB=1/2*180=90 độ
Xét tứ giác BDIH có
góc IHB+góc IDB=180 độ
=>BDIH là tứ giác nội tiếp
b: góc IDH=góc IBH=1/2*sđ cung AC=góc ADC
=>DA là phân giác của góc CDH
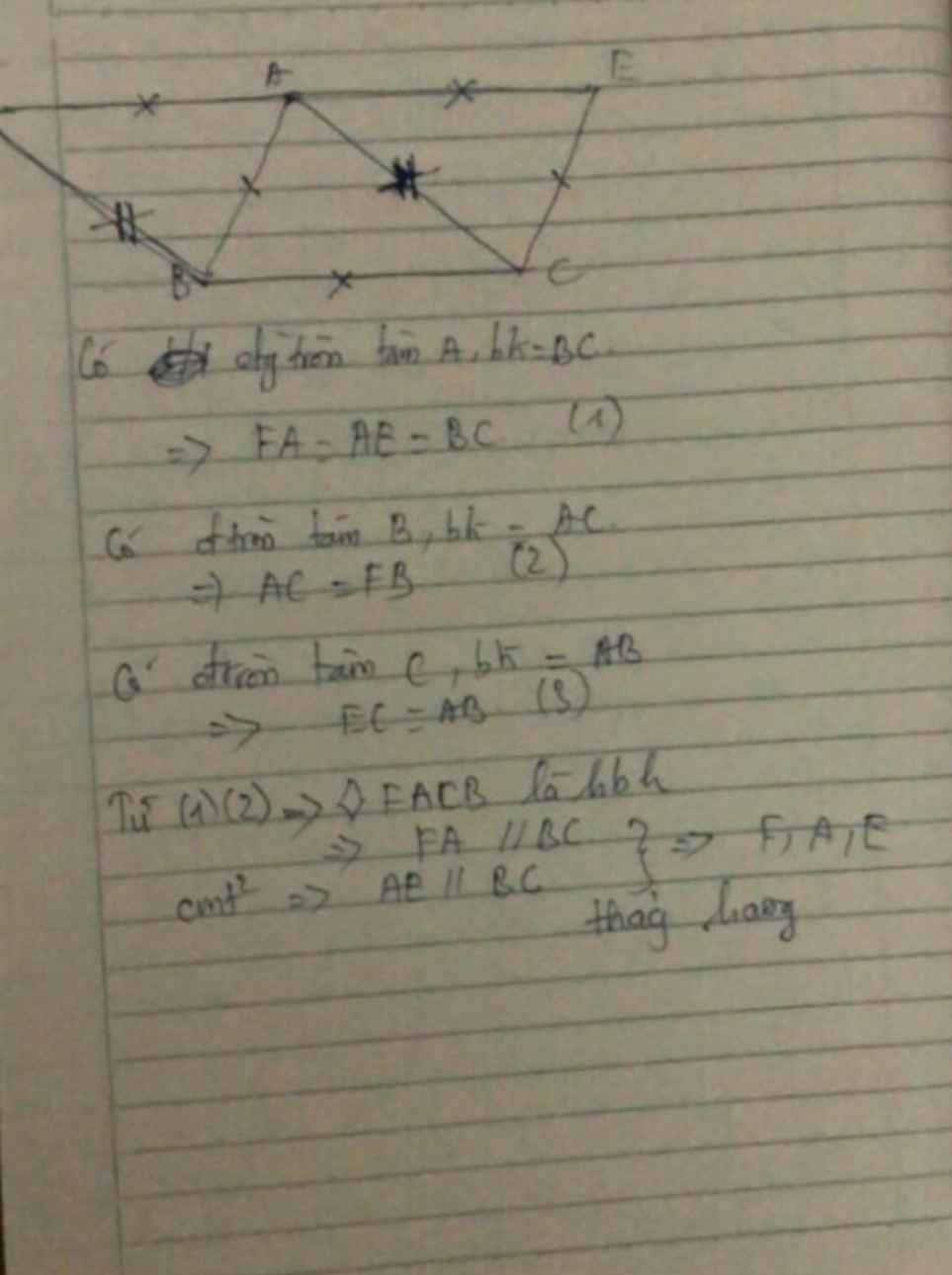
tam giac abd bằng tam giac ace (c.g.c)
nên góc bad=góc cae
tam giac abi=tam giac acj(g,c,g)
nên bi=cj(1)
gọi o là trung điểm bc
vì góc oda=góc bad(=60-góc adb)
nên od//ab nên \(\frac{oi}{ib}=\frac{od}{ab}=\frac{od}{2ob}=\frac{1}{2}\)
nên oi=\(\frac{1}{2}\)ib hay 2oi=ib
nên ij=ib(2)
từ (1) và (2) suy ra bi=ij=jc