Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Xác định góc giữa hai đường thẳng MN và AP
A. 60
B. 90
C. 30
D. 45
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
3 tháng 7 2018
Đúng(0)
Những câu hỏi liên quan
G
10 tháng 8 2023
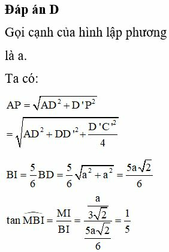
\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A
CM
13 tháng 3 2017
Chọn D.
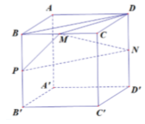
Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN). Do đó:
d(MN;BD) = d(BD;(MPN)) = d(B;(MPN))
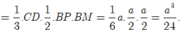
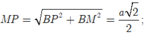
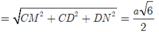
Nhận thấy 
nên tam giác MPN vuông tại M.
Do đó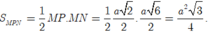 
Ta có 
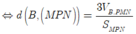
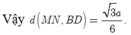
Cách 2:
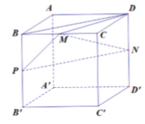
Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN).
Đồng thời, MP//CB', PN//B'D' => (MPN)//(CB'D')
Do đó 
(vì PC’ cắt B’C tại trọng tâm tam giác BB’C’).
Nhận thấy tứ diện C'.CB'D' là tứ diện vuông tại C' nên
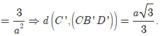
Vậy 
Cách 3: Tọa độ hóa
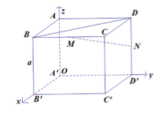
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó,
CM
10 tháng 2 2017
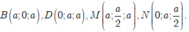
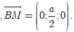
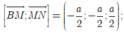
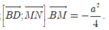
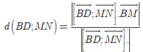
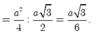
Chọn đáp án C.
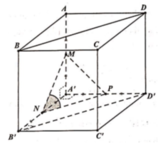
Gọi P là trung điểm cạnh A'D' khi đó BD//NP.
Khi đó góc giữa 
Vì ABCD.A'B'C'D' là hình lập phương cạnh a nên 
Suy ra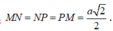 
Do đó tam giác MNP đều 
