Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án D
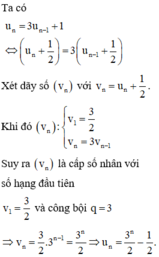
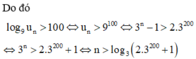
Vậy số tự nhiên n nhỏ nhất thỏa mãn điều kiện trên là n 0 = 201
\(C^n_n+C^{n-1}_n+C^{n-2}_n=37\)
\(\Leftrightarrow1+\dfrac{n!}{\left(n-1\right)!}+\dfrac{n!}{\left(n-2\right)!2!}=37\)
\(\Leftrightarrow1+n+\dfrac{n\left(n-1\right)}{2}=37\)
\(\Rightarrow n=8\)
\(P=\left(2+5x\right)\left(1-\dfrac{x}{2}\right)^8=\left(2+5x\right).\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{x}{2}\right)^k\right)\)
\(=\left(2+5x\right).\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)\)
\(=2.\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)+5x\)\(\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)\)
\(=2.\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)+5\)\(\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^{k+1}\right)\)
Số hạng chứa \(x^3\) trong \(2.\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)\) là \(2C^3_8.\left(-\dfrac{1}{2}\right)^3x^3\)
Số hạng chứa \(x^3\) trong \(5\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^{k+1}\right)\) là \(5C^2_8.\left(-\dfrac{1}{2}\right)^2x^3\)
Vậy số hạng chứa x3 trong P là:\(\left[2.C^3_8\left(-\dfrac{1}{2}\right)^3+5C^2_8\left(-\dfrac{1}{2}\right)^2\right]x^3\)
Xài cái này gõ bài đi bạn, thề như này hiểu chết liền á :(
Đáp án là C