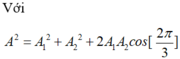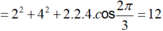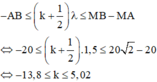Hai nguồn kết hợp được đặt ở A và B trên mặt thoáng của chất lỏng, dao động theo phương vuông góc với mặt thoáng có phương trình u A = 2 cos 40 πt cm , u B = 4 cos 40 πt cm với t tính theo giây. Tốc độ truyền sóng bằng 90 cm/s. Gọi M là một điểm nằm trên mặt thoảng với MA = 10,5 cm; MB = 9 cm. Coi biên độ không thay đổi trong quá trình truyền sóng. Phần tử chất lỏng tại M dao động với biên độ là
A. 6 cm
B. 2 , 5 3 c m
C. 2 cm.
D. 2 3 c m