Cho tứ diện đều ABCD có M, N lần lượt là trung điểm của các cạnh AB và CD. Mệnh đề nào sau đây sai?
A. M N ⊥ C D .
B. A B ⊥ C D .
C. M N ⊥ A B .
D. M N ⊥ B D .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
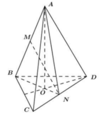
Phương pháp:
+) Tứ diện đều ABCD có tất cả các cạnh đều bằng nhau.
+) Hình chiếu của đỉnh A trên mặt phẳng (BCD) là trọng tâm O của tam giác BCD.
Cách giải:

ABCD là tứ diện đều nên có các mặt là các tam giác đều và bằng nhau.


Chọn D.
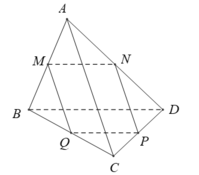
- Vì MN, PQ lần lượt là đường trung bình tam giác ABD, BCD nên:
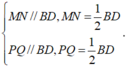
- Nên MN // PQ, MN = PQ.
⇒ tứ giác MNPQ là hình bình hành.
- Do đó MP và NQ cùng thuộc mặt phẳng MNPQ và hai đường thẳng này cắt nhau.

Ta có:
\(\left. \begin{array}{l}J \in C{\rm{D}}\\C{\rm{D}} \subset \left( {IC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {IC{\rm{D}}} \right)\).
Vậy bốn điểm \(I,J,C,D\) đồng phẳng.
Chọn D.
Đáp án D