Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Số hạt U238 đã phân rã bằng số hạt alpha tạo thành:
Thời gian rất ngắn nên
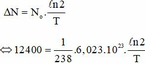
≈ 4,5 tỉ năm.
Chọn đáp án A
Số hạt nhân Chì sinh ra bằng số hạt nhân Pôlôni đã phân rã
N P b = Δ N = N 0 − N = N 0 1 − 2 − t T
Tỉ số hạt nhân Chì và số hạt nhân Pôlôni ở thời điểm t là:
N P b N P o = N 0 1 − 2 − t T N 0 .2 − t T = 2 t T − 1 → N = m A . N A m P b m P o = A P b A P o 2 t T − 1 = 206 210 2 1 138 − 1 = 0 , 6 ⇒ t = T log 2 0 , 6.210 206 + 1 ≈ 95
Chú ý: Có thể giải phương trình trên bằng cách bấm máy tính cầm tay.
Chọn đáp án A
Ta có phương trình phản ứng: 84 210 P o → 2 4 α + 82 206 P b
Khối lượng Po còn lại sau thời gian t: m P o = m 0 2 − t T
Khối lượng chì sinh ra: m P b = m c o n = A c o n A m e 1 − 2 − t T m 0 = 206 210 1 − 2 − t T m 0
Theo đề: m P b m P o = 206 210 1 − 2 − t T 2 − t T = 206 210 2 t T − 1 = 0 , 6 ⇒ t ≈ 95 n g à y
Chọn đáp án A.
Giả sử lượng Poloni ban đầu là N0
=> Sau đó là N = N 0 . 2 - t T
Như vậy, lượng Po bị phân rã là: N0 – N
=> Lượng chỉ sinh ra là: N0 – N
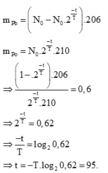
Đáp án B