Cho lục giác đều ABCDEF có cạnh bằng 4. Quay lục giác đều đó quanh đường thẳng AD. Tính thể tích V của khối tròn xoay được sinh ra.
A. V = 128 π
B. V = 32 π
C. V = 16 π
D. V = 64 π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
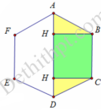
Khi quay lục giác đã cho quanh AD ta được 2 hình nón và một hình trụ
Hình trụ có chiều cao h = B C = 4 và bán kính đáy r = B H = 4 3 2 = 2 3
Hình nón có chiều cao h ' = A H = 2 và bán kính đáy r = B H = 2 3
Khi đó V = π r 2 h + 2 3 π r 2 h ' = 64 π .

Gọi thể tích của khối tròn xoay là V, thể tích
khối nón là V 1 và thể tích của khối trụ là V 2 .
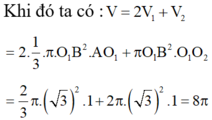

Đáp án: B
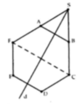
Khối tròn xoay được tạo thành bởi lục giác ABCDEF có thể tích gấp đôi khối tròn xoay (H) được tạo thành bởi hình thang ABCF.
Gọi V* là thể tích của khối nón tạo bởi tam giác đều SAB
Do đó ta có: V = 2 V ( H ) và
V ( H ) = 8 V * - V * = 7 V * = 7 πa 3 3 24
Kết luận: ta có thể tích cần tìm là

Đáp án D
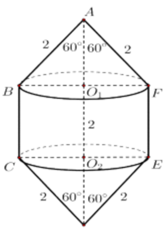
Khi quay lục giác đều đã cho quanh AD ta được 2 hình nón và 1 hình trụ
Hình trục có chiều cao h = B C = 4.
Bán kính đáy r = B H = 4 3 2 = 2 3 .
Hình nón có chiều cao h ' = A H = 2 , bán kính đáy r = B H = 2 3 ; V = π r 2 h + 2 3 π r 2 h ' = 64 π